Question

设A，B，C为单位圆O上不同的三点，则点集A={(x，y)|

OC

=x

OA

+y

OB

，0＜x＜2，0＜y＜2}所对应的平面区域的面积为（　　）

• A、1
• B、

  3

  2

• C、2
• D、

  5

  2

Answer 1

分析：利用数量积的性质将

OC

=x

OA

+y

OB

两边平方，再利用已知|

OA

|=|

OB

|=|

OC

|=1，化为
1=x²+y²+2xycos∠AOB，由于0＜x＜2，0＜y＜2．从而由余弦定理可知x、y、1可以构成三角形，且∠AOB不是0°或180°．得到约束条件，画出可行域即可得出．

解答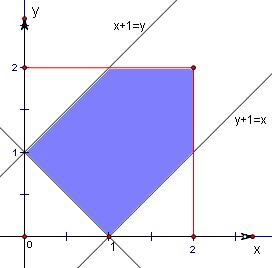：解：将

OC

=x

OA

+y

OB

两边平方得：

OC

2=x2

OA

2+y2

OB

2+2xy

OA

•

OB

cos∠AOB．
∵|

OA

|=|

OB

|=|

OC

|=1，
∴1=x²+y²+2xycos∠AOB，
∵0＜x＜2，0＜y＜2．
从而由余弦定理可知x、y、1可以构成三角形，且∠AOB不是0°或180°．
于是有：

|x|+|y|≥1 |x|+1≥|y| |y|+1≥|x| 0＜x＜2，0＜y＜2

，化为

x+y≥1 x+1≥y y+1≥x 0＜x＜2，0＜y＜2

画出平面区域，结合图形可知约束条件表示的图形为阴影区域内，
∴表示的平面区域的面积是4-3×

1

2

=

5

2

．
故答案为：

5

2

．

点评：本题考查了数量积的性质、余弦定理、构成三角形的条件、线性规划问题，考查了问题的转化能力，属于难题．