Question

设A，B，C为单位圆O上不同的三点，则点集A={（x，y）|

OC

=x

OA

+y

OB

，（0＜x＜2，0＜y＜2）}所对应的平面区域的面积为

5

2

．

Answer 1

分析：先根据约束条件画出满足条件的平面区域，然后结合图形可知约束条件表示的图形，最后求出其面积即可．

解答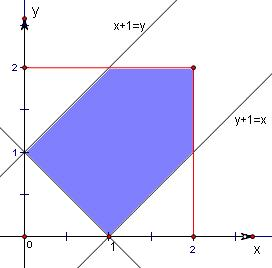：解：将

OC

=x

OA

+y

OB

平方得：OC²=x²OA²+y²OB²+2xyOA×OBcos∠AOB．
即1=x²+y²+2xycos∠AOB，
从而由余弦定理可知|x|、|y|、1可以构成三角形，且∠AOB不是0°或180°．
于是有：

|x|+|y|≥1 |x|+1≥|y| |y|+1≥|x| 0＜x＜2，0＜y＜2

，即

x+y≥1 x+1≥y y+1≥x 0＜x＜2，0＜y＜2

画出平面区域，结合图形可知约束条件表示的图形为阴影区域内，
∴表示的平面区域的面积是4-3×

1

2

=

5

2

故答案为：

5

2

．

点评：本题主要考查了两个知识点：平面向量的坐标运算以及一元二次不等式组所表示的平面区域，同时考查了阅读理解题意的能力以及简单的转化思想和数形结合的思想，属中档题．