题目内容
斜三棱柱ABC-A′B′C′中,底面是边长为a的正三角形,侧棱长为 b,侧棱AA′与底面相邻两边AB、AC都成45°角,求此三棱柱的侧面积和体积.
分析:(1)先判断斜三棱柱ABC-A′B′C′的三个侧面的形状,分别求出面积再相加,即为斜三棱柱的侧面积.
(2)斜三棱柱的体积等于底面积乘高,因为底面三角形是边长为a的正三角形,面积易求,所以只需求出高即可,利用所给线线角的大小即可求出.
(2)斜三棱柱的体积等于底面积乘高,因为底面三角形是边长为a的正三角形,面积易求,所以只需求出高即可,利用所给线线角的大小即可求出.
解答:解:(1)∵侧棱AA′与底面相邻两边AB、AC都成45°角,
∴三棱柱的三个侧面中,四边形ABBA和ACCA是有一个角是45°,相邻两边长分别为a,b的平行四边形,第三个侧面是边长分别为a,b的矩形.
∴s侧=2absib45°+ab=(
+1)ab
(2)过A1作A1O垂直于底面ABC,交底面ABC于O点,作A1D⊥AB,交AB于D点,连接DO,由题意,则
AD=
,A1D=
,∴AO=
,A1O=
∴V=
×
a
=
a2b
∴三棱柱的三个侧面中,四边形ABBA和ACCA是有一个角是45°,相邻两边长分别为a,b的平行四边形,第三个侧面是边长分别为a,b的矩形.
∴s侧=2absib45°+ab=(
| 2 |
(2)过A1作A1O垂直于底面ABC,交底面ABC于O点,作A1D⊥AB,交AB于D点,连接DO,由题意,则
AD=
| ||
| 2 |
| ||
| 2 |
| ||
| 3 |
| ||
| 3 |
∴V=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
| 1 |
| 4 |
点评:本题主要考查了斜三棱柱的侧面积与体积的求法,属于立体几何的基础题.

练习册系列答案
相关题目
 (2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=
(2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=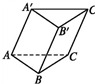 如图,斜三棱柱ABC-A′B′C′中,底面是边长为a的正三角形,侧棱长为b,侧棱AA′与底面相邻两边AB,AC都成45°角.
如图,斜三棱柱ABC-A′B′C′中,底面是边长为a的正三角形,侧棱长为b,侧棱AA′与底面相邻两边AB,AC都成45°角.