题目内容
已知函数f(x)=x2-x+t,t≥0,g(x)=lnx.
(1)令h(x)=f(x)+g(x),求证:h(x)是增函数;
(2)直线l与函数f(x),g(x)的图象都相切.对于确定的正实数t,讨论直线l的条数,并说明理由.
解:(1)由h(x)=f(x)+g(x)=x2-x+t+lnx,得h' (x)=2x-1+ ,x>0.
,x>0.
因为2x+ ≥2
≥2 =2
=2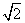 ,所以h' (x)>0,
,所以h' (x)>0,
从而函数h(x)是增函数.
(2)记直线l分别切f(x),g(x)的图象于点(x1,x12-x1+t),(x2,lnx2),
由f'(x)=2x-1,得l的方程为y-(x12-x1+t)=(2x1-1)(x-x1),即y=(2x1-1)x-x12+t.
由g'(x)= ,得l的方程为y-lnx2=
,得l的方程为y-lnx2= (x-x2),即y=
(x-x2),即y= · x+lnx2-1.
· x+lnx2-1.
 x>0.
x>0.
由F'(x)=0,解得x=1.
当0<x<1时,F'(x)<0,当x>1时,F'(x)>0,
所以F(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
从而F(x)min=F(1)=-t.
当t=0时,方程(**)只有唯一正数解,从而方程组(*)有唯一一组解,
即存在唯一一条满足题意的直线;
当t>0时,F(1)<0,由于F(et+1)>ln(et+1)-(t+1)=0,
故方程(**)在(1,+∞)上存在唯一解;
令k(x)=lnx+ -1(x≤1),由于k' (x)=
-1(x≤1),由于k' (x)= -
- =
= ≤0,故k (x)在(0,1]上单调递减,
≤0,故k (x)在(0,1]上单调递减,
 故方程(**)在(0,1)上存在唯一解.
故方程(**)在(0,1)上存在唯一解.
所以当t>0时,方程(**)有两个不同的正数解,方程组(*)有两组解.
即存在两条满足题意的直线.
综上,当t=0时,与两个函数图象同时相切的直线的条数为1;
当t>0时,与两个函数图象同时相切的直线的条数为2.

 阅读快车系列答案
阅读快车系列答案 4+3x-x2)的单调递减区间是________________.
4+3x-x2)的单调递减区间是________________. .
. 的值.
的值.
 =1的右焦点F作x轴的垂线l,则l与双曲线C的两条渐近线所围成的三角形的面积是 .
=1的右焦点F作x轴的垂线l,则l与双曲线C的两条渐近线所围成的三角形的面积是 .  ≥2y+3.
≥2y+3.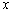 ,
, 满足
满足 则
则 的最大值是 .
的最大值是 . ,则在复平面内,复数
,则在复平面内,复数 对应的点位于 ( )
对应的点位于 ( ) ,其中
,其中 .
. 的单调性;
的单调性; 在
在 上恒成立,求实数
上恒成立,求实数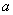 的取值范围.
的取值范围.