题目内容
3.方程2x-x=$\frac{3}{2}$有2个实数根.分析 由2x-x=$\frac{3}{2}$得2x=x+$\frac{3}{2}$,然后在同一坐标系中画出y=2x与y=x+$\frac{3}{2}$的图象,利用图象的交点可以求出函数零点个数.
解答 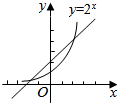 解:由2x-x=$\frac{3}{2}$得2x=x+$\frac{3}{2}$,令y=2x,y=x+$\frac{3}{2}$
解:由2x-x=$\frac{3}{2}$得2x=x+$\frac{3}{2}$,令y=2x,y=x+$\frac{3}{2}$
在同一坐标系中画出y=2x与y=x+$\frac{3}{2}$的图象如图所示.
由图象可知y=2x与y=x+$\frac{3}{2}$有两个交点,
故方程2x-x=$\frac{3}{2}$在实数范围内有两解.
故答案为:2.
点评 本题主要考查函数的零点个数,解决本题的关键是利用数形结合的思想去解决.

练习册系列答案
相关题目
13.现有4件不同款式的上衣与3件不同颜色的长裤,如果一条长裤和一件上衣配成一套,则不同选法是( )
| A. | 7 | B. | 64 | C. | 12 | D. | 81 |
18.函数y=2-x-1+1的图象可以由函数y=2-x的图象( )
| A. | 先向右平移1个单位,再向上平移1个单位得到 | |
| B. | 先向左平移1个单位,再向上平移1个单位得到 | |
| C. | 先向右平移1个单位,再向下平移1个单位得到 | |
| D. | 先向左平移1个单位,再向下平移1个单位得到 |