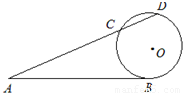
题目内容
已知圆O的半径为2,PA,PB为该圆的两条切线,A,B为两切点,设∠APO=α.那么2S△PAB•cot2α的最小值为( )
分析:由题意画出图形,求出PA,PO,A到PO的距离为AC,PC,求出S△PAB.得到2S△PAB•cot2α,化简利用基本不等式求出最小值.
解答: 解:由题意PA=
解:由题意PA=
,PO=
A到PO的距离为AC=2cosα,PC=
•cosα
所以S△PAB=2×
PC•AC=
•2cosα•cosα.
2S△PAB•cot2α=
•2cosα•cosα•cot2α
=
=
=
-12+8sin2α≥-12+8
,当且仅当sin4α=
时,取等号.
故选D.
 解:由题意PA=
解:由题意PA=| 2 |
| tanα |
| 2 |
| sinα |
A到PO的距离为AC=2cosα,PC=
| 2 |
| tanα |
所以S△PAB=2×
| 1 |
| 2 |
| 2 |
| tanα |
2S△PAB•cot2α=
| 4 |
| tanα |
=
| 4cos2α•(1-2sin2α) |
| sin2α |
=
| 4(1-sin2α)(1-2sin2α) |
| sin2α |
=
| 4 |
| sin2α |
| 2 |
| 1 |
| 2 |
故选D.
点评:本题考查直线与圆的位置关系,三角形的面积的求法,三角函数的化简以及基本不等式的应用,考查计算能力.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
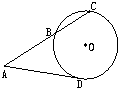 如图,已知圆O的半径为2,从圆O外一点A引切线AD和割线ABC,圆心O到AC的距离为
如图,已知圆O的半径为2,从圆O外一点A引切线AD和割线ABC,圆心O到AC的距离为 (2013•肇庆一模)(几何证明选讲选做题)
(2013•肇庆一模)(几何证明选讲选做题)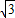 ,AB=3,则切线AD的长为 .
,AB=3,则切线AD的长为 .
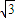 ,
,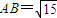 ,则AC的长为 .
,则AC的长为 .