题目内容
已知一个三棱柱,其底面是正三角形,且侧棱与底面垂直,一个体积为 的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是
的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是
- A.

- B.
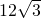
- C.

- D.
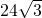
C
分析:由球的体积可以求出半径,从而得棱柱的高;由球与正三棱柱的三个侧面相切,得球的半径和棱柱底面正△边长的关系,求出边长,即求出底面正△的面积;得出棱柱的表面积.
解答:由球的体积公式,得 πR3=
πR3= ,
,
∴R=1.
∴正三棱柱的高h=2R=2.
设正三棱柱的底面边长为a,则其内切圆的半径为: •
• a=1,
a=1,
∴a=2 .
.
∴该正三棱柱的表面积为:3a•2R+2× =18
=18 .
.
故选C.
点评:本题考查了球的体积,柱体体积公式的应用;本题的解题关键是求底面边长,这是通过正△的内切圆与边长的关系得出的.
分析:由球的体积可以求出半径,从而得棱柱的高;由球与正三棱柱的三个侧面相切,得球的半径和棱柱底面正△边长的关系,求出边长,即求出底面正△的面积;得出棱柱的表面积.
解答:由球的体积公式,得
 πR3=
πR3= ,
,∴R=1.
∴正三棱柱的高h=2R=2.
设正三棱柱的底面边长为a,则其内切圆的半径为:
 •
• a=1,
a=1,∴a=2
 .
.∴该正三棱柱的表面积为:3a•2R+2×
 =18
=18 .
.故选C.
点评:本题考查了球的体积,柱体体积公式的应用;本题的解题关键是求底面边长,这是通过正△的内切圆与边长的关系得出的.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是( )
的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是( ) B.
B. C.
C.  D.
D. 
 的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是( )
的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是( )



 的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是( )
的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是( )


