题目内容
函数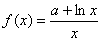 ,若曲线
,若曲线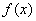 在点
在点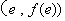 处的切线与直线
处的切线与直线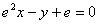 垂直(其中
垂直(其中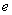 为自然对数的底数).
为自然对数的底数).
(1)若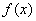 在
在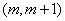 上存在极值,求实数
上存在极值,求实数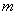 的取值范围;
的取值范围;
(2)求证:当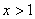 时,
时,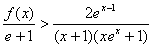 .
.
【解析】(1) ;(2)见解析
;(2)见解析
解析:(1)∵
由已知 ∴
∴ 得
得 ………2分
………2分
∴
当 为增函数;
为增函数;
当 时,
时, ,
,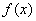 为减函数。
为减函数。
∴ 是函数
是函数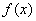 的极大值点 ………4分
的极大值点 ………4分
又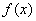 在
在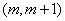 上存在极值
上存在极值
∴  即
即
故实数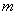 的取值范围是
的取值范围是 ………5分
………5分
(2) 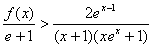
即为 ………6分
………6分
令
则
再令 则
则
∵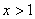 ∴
∴ ∴
∴  在
在 上是增函数
上是增函数
∴ ∴
∴
∴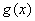 在
在 上是增函数
上是增函数
∴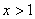 时,
时, 故
故 ………9分
………9分
令

则
∵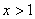 ∴
∴ ∴
∴ 即
即
 上是减函数
上是减函数
∴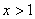 时,
时, ………11分
………11分
所以 , 即
, 即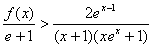 ………12分
………12分
【思路点拨】(1)先求导得 ,利用单调性判断出
,利用单调性判断出 是函数
是函数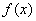 的极大值点,所以有
的极大值点,所以有 ,解不等式组即可;(2)先转化为
,解不等式组即可;(2)先转化为 , 令
, 令 ,再求导结合单调性证明。
,再求导结合单调性证明。

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
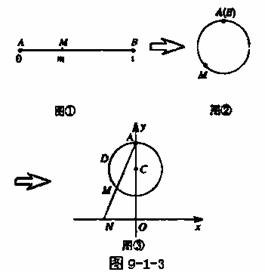
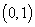 到实数集
到实数集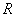 的映射过程:区间
的映射过程:区间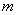 对应数轴上的点
对应数轴上的点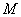 ,如图9-2中的图①;将线段
,如图9-2中的图①;将线段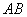 围成一个圆,使两端点
围成一个圆,使两端点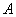 、
、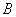 恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在
恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在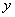 轴上,点
轴上,点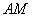 与
与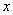 轴交于点
轴交于点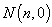 ,则
,则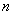 ,记作
,记作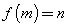 .
.
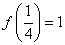 ; ②
; ②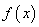 是奇函数;
是奇函数; 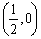 对称.
对称.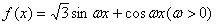 的图象与
的图象与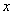 轴交点的横坐标构成一个公差为
轴交点的横坐标构成一个公差为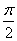 的等差数列,把函数
的等差数列,把函数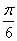 个单位,得到函数
个单位,得到函数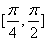 上是增函数 B. 其图象关于直线
上是增函数 B. 其图象关于直线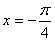 对称
对称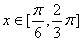 时,函数
时,函数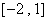
 的前
的前 项和为
项和为 ,且
,且 ,
, 为等差数列,则
为等差数列,则 ____________.
____________. ,集合
,集合 ,则下图阴影部分表示的集合是()
,则下图阴影部分表示的集合是() 
 满足
满足 ,则函数
,则函数 的零点所在的区间是
的零点所在的区间是 B.
B.  C.
C.  D.
D.
 ,且
,且 ,则集合
,则集合 可能是( )
可能是( ) (B)
(B) (C)
(C) (D)
(D) 
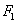 、
、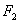 为椭圆
为椭圆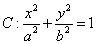 的左、右焦点,
的左、右焦点,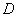 、
、 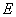 是椭圆的两个顶点,椭圆的离心率
是椭圆的两个顶点,椭圆的离心率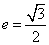 ,
,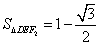 .若
.若 在椭圆
在椭圆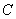 上,则点
上,则点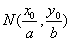 称为点
称为点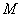 的一个“好点”.直线
的一个“好点”.直线 与椭圆交于
与椭圆交于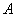 、
、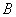 两点,
两点, 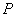 、
、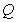 ,已知以
,已知以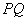 为直径的圆经过坐标原点.
为直径的圆经过坐标原点.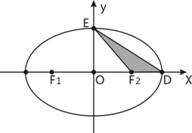
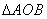 的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.
的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.