题目内容
函数 的图象为C,有如下结论:
的图象为C,有如下结论:
①图象C关于直线 对称;
对称;
②图象C关于点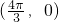 对称;
对称;
③函数f(x)在区间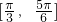 内是增函数,
内是增函数,
其中正确的结论序号是________.(写出所有正确结论的序号)
①②③
分析:由题意可解出该函数的所有对称轴,对称区间和单调递增区间,取整数k的特殊值,比较选项即可得答案.
解答:由 =kπ+
=kπ+ ,可得x=kπ+
,可得x=kπ+ ,k∈Z,
,k∈Z,
当k=0时,可得其中一条对称轴为x= ,故①正确;
,故①正确;
由 =kπ,可得x=kπ+
=kπ,可得x=kπ+ ,k∈Z,
,k∈Z,
当k=1时,可得其中一个对称点的横坐标为x= ,故②正确;
,故②正确;
由2kπ- ≤
≤ ≤2kπ+
≤2kπ+ 得2kπ-
得2kπ- ≤x≤2kπ+
≤x≤2kπ+ ,k∈Z,
,k∈Z,
当k=0时,可得其中一个单调递增区间为[ ,
, ],
],
因为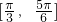 真包含于[
真包含于[ ,
, ],
],
所以函数在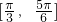 上单调递增,故③正确.
上单调递增,故③正确.
故答案为:①②③
点评:本题考查命题真假的判断,涉及三角函数的对称性和单调性,属基础题.
分析:由题意可解出该函数的所有对称轴,对称区间和单调递增区间,取整数k的特殊值,比较选项即可得答案.
解答:由
 =kπ+
=kπ+ ,可得x=kπ+
,可得x=kπ+ ,k∈Z,
,k∈Z,当k=0时,可得其中一条对称轴为x=
 ,故①正确;
,故①正确;由
 =kπ,可得x=kπ+
=kπ,可得x=kπ+ ,k∈Z,
,k∈Z,当k=1时,可得其中一个对称点的横坐标为x=
 ,故②正确;
,故②正确;由2kπ-
 ≤
≤ ≤2kπ+
≤2kπ+ 得2kπ-
得2kπ- ≤x≤2kπ+
≤x≤2kπ+ ,k∈Z,
,k∈Z,当k=0时,可得其中一个单调递增区间为[
 ,
, ],
],因为
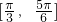 真包含于[
真包含于[ ,
, ],
],所以函数在
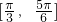 上单调递增,故③正确.
上单调递增,故③正确.故答案为:①②③
点评:本题考查命题真假的判断,涉及三角函数的对称性和单调性,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的图象为C,有如下结论:
的图象为C,有如下结论: 对称;
对称; 对称;
对称; 内是增函数,
内是增函数, 的图象为C,有如下结论:
的图象为C,有如下结论: 对称;
对称; 对称;
对称; 内是增函数,
内是增函数,