题目内容
已知数列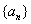 是等差数列
是等差数列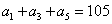 ,
,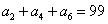 ,
,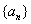 的前
的前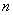 项和为
项和为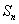 ,则使得
,则使得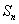 达到最大的
达到最大的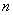 是( )
是( )
| A.18 | B.19 | C.20 | D.21 |
C
解析试题分析:根据题意,由于数列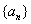 是等差数列
是等差数列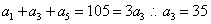 ,
,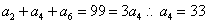 ,故可知公差为-2,那么可知首项为35+4=39,那么根据前n项和公式可知,
,故可知公差为-2,那么可知首项为35+4=39,那么根据前n项和公式可知,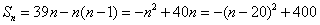 ,根据二次函数性质可知n=20时函数值最大,及前20项和最大,故选C.
,根据二次函数性质可知n=20时函数值最大,及前20项和最大,故选C.
考点:等差数列
点评:主要是考查了等差数列的通项公式和求和的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
等差数列{an}中,已知a1=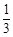 ,a2+a5=4,an=33,则n的值为( ).
,a2+a5=4,an=33,则n的值为( ).
| A.50 | B.49 | C.48 | D.47 |
等差数列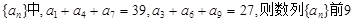 项的和
项的和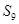 等于
等于
A.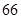 | B.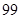 | C.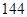 | D.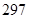 |
已知等差数列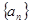 的公差为
的公差为 ,若其前13项和
,若其前13项和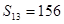 ,则
,则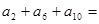 ( )
( )
| A.36 | B.39 | C.42 | D.45 |
等差数列{an}中,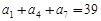 ,
, ,则数列{an}前9项的和
,则数列{an}前9项的和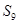 等于( )
等于( )
A. | B. | C. | D.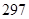 |
已知数列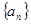 中, a2=7,且an =an+1-6(n∈
中, a2=7,且an =an+1-6(n∈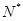 ),则前n项和Sn=" (" )
),则前n项和Sn=" (" )
A.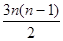 | B. n2 | C.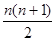 | D.3n2 –2n |
设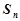 是等差数列
是等差数列 的前
的前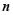 项和,若
项和,若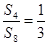 ,则
,则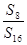 等于( )
等于( )
A.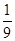 | B.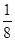 | C.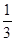 | D.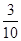 |
首项为 的等差数列,从第10项起开始为正数,则公差
的等差数列,从第10项起开始为正数,则公差 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
已知等差数列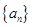 的前
的前 项和为
项和为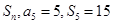 ,则数列
,则数列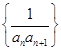 的前100项和为( )
的前100项和为( )
A.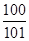 | B.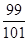 | C.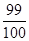 | D.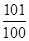 |