题目内容
设O为坐标原点,F1,F2是椭圆 (a>b>0)的焦点,若在椭圆上存在点P,满足∠F1PF2=60°,|OP|=
(a>b>0)的焦点,若在椭圆上存在点P,满足∠F1PF2=60°,|OP|=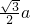 ,则该椭圆的离心率为
,则该椭圆的离心率为
- A.

- B.

- C.

- D.

A
分析:要求椭圆的离心率,即要求a,c的关系,首先由定义和余弦定理得到一个关系,再由中线长公式得到一个关系,联立可得.
解答:设|PF1|=x,|PF2|=y,则x+y=2a;①
由余弦定理 cos∠F1PF2= ?
? =
= ;
;
∴x2+y2-xy=4c2;②
∵中线长公式 =
= (
(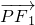 +
+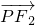 )
)
故OP2= (PF12+PF22+2
(PF12+PF22+2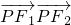 )
)
? =
= (x2+y2+2xycos∠F1PF2)?x2+y2=3a2-xy;③
(x2+y2+2xycos∠F1PF2)?x2+y2=3a2-xy;③
∴①②③联立代换掉x,y得:a2=4c2;
∴ =
= .
.
故选:A.
点评:本题主要考查椭圆的定义,余弦定理及中线长公式,体现了在解题中要灵活运用转化知识.
分析:要求椭圆的离心率,即要求a,c的关系,首先由定义和余弦定理得到一个关系,再由中线长公式得到一个关系,联立可得.
解答:设|PF1|=x,|PF2|=y,则x+y=2a;①
由余弦定理 cos∠F1PF2=
 ?
? =
= ;
;∴x2+y2-xy=4c2;②
∵中线长公式
 =
= (
(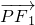 +
+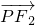 )
)故OP2=
 (PF12+PF22+2
(PF12+PF22+2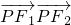 )
)?
 =
= (x2+y2+2xycos∠F1PF2)?x2+y2=3a2-xy;③
(x2+y2+2xycos∠F1PF2)?x2+y2=3a2-xy;③∴①②③联立代换掉x,y得:a2=4c2;
∴
 =
= .
.故选:A.
点评:本题主要考查椭圆的定义,余弦定理及中线长公式,体现了在解题中要灵活运用转化知识.

练习册系列答案
相关题目
设O为坐标原点,F1,F2是双曲线
-
=1(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠F1PF2=60°,|OP|=
a,则该双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
A、x±
| ||
B、
| ||
C、x±
| ||
D、
|