题目内容
若 是定义在
是定义在 上的增函数,且
上的增函数,且
(1)、求 的值;(2)、若
的值;(2)、若 ,解不等式
,解不等式 .
.
 是定义在
是定义在 上的增函数,且
上的增函数,且
(1)、求
 的值;(2)、若
的值;(2)、若 ,解不等式
,解不等式 .
.(1) ; (2)
; (2)
 ; (2)
; (2)
试题分析:(1)结合
 通过赋值可得
通过赋值可得 ;(2)先由抽象函数的性质可求得
;(2)先由抽象函数的性质可求得 ,从而将不等式转化为
,从而将不等式转化为 故
故 ,再利用函数的单调性和定义域解得
,再利用函数的单调性和定义域解得 的取值范围,即:
的取值范围,即: .本题注意通过赋值处理抽象函数的方法,易错点是容易漏掉函数定义域的考虑.
.本题注意通过赋值处理抽象函数的方法,易错点是容易漏掉函数定义域的考虑.试题解析:⑴在等式中令
 ,则
,则 ; 3分
; 3分⑵在等式中令
 则
则 ,
, , 7分
, 7分故原不等式为:
 即
即 ,
,又
 在
在 上为增函数,故原不等式等价于:
上为增函数,故原不等式等价于:
即:
 12分
12分
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 在[-1,1]上的最大值为M(a),则函数g(x)=M(x)-
在[-1,1]上的最大值为M(a),则函数g(x)=M(x)- 的零点个数为
的零点个数为 的方程
的方程 有两个不同的解,则
有两个不同的解,则 的取值范围是( )
的取值范围是( )



 是方程
是方程 的解,则
的解,则



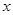 的方程
的方程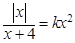 有四个不同的实数解,则实数k的取值范围是 .
有四个不同的实数解,则实数k的取值范围是 . 、
、 是方程
是方程 ,
, 的解,函数
的解,函数 ,则关于
,则关于 的方程
的方程 的解的个数是( )
的解的个数是( )



 的方程
的方程 只有一个实数解,则实数
只有一个实数解,则实数 的取值范围是_______.
的取值范围是_______. 上的奇函数
上的奇函数 ,满足
,满足 ,
, ,则函数
,则函数 在区间
在区间 内零点个数的情况为( )
内零点个数的情况为( ) 个
个 个
个 个
个