题目内容
在正三角形ABC中,E、F分别是AB、AC边上的点,满足将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连结A1B、A1C.(如图(2))
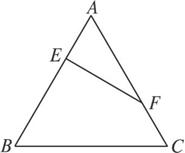
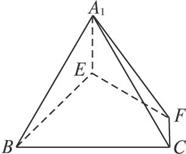
(1) (2)
(1)求证:A1E⊥平面BEC;
(2)求直线A1E与平面A1BC所成角的大小.
解:不妨设正三角形ABC的边长为3,则
(1)证明:在题图(1)中,取BE中点D,连结DF,
∵![]() =
=![]() =
=![]() ,∴AE=1,AF=2,而∠A=60°.∴EF⊥AE.
,∴AE=1,AF=2,而∠A=60°.∴EF⊥AE.
∴在题图(2)中有A1E⊥EF,BE⊥EF.
∴∠A1EB为二面角A1EFB的平面角.
∵二面角A1EFB为直二面角,
∴A1E⊥BE.
又∵BE∩EF=E,∴A1E⊥平面BEC.
(2)过E作EH⊥BC于H,连结A1H,作EO⊥A1H于O,证明EO⊥平面A1BC,在直角三角形A1EH中求得直线A1E与平面A1BP所成角的大小为![]() .
.

练习册系列答案
相关题目
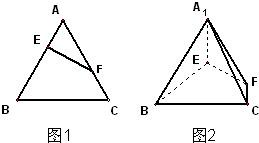 在正三角形ABC中,E、F分别是AB、AC边上的点,满足
在正三角形ABC中,E、F分别是AB、AC边上的点,满足 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,J分别为AF,DE的中点.将△ABC沿DE,EF,DF折成三棱锥以后,GJ与DE所成角的度数为( )
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,J分别为AF,DE的中点.将△ABC沿DE,EF,DF折成三棱锥以后,GJ与DE所成角的度数为( )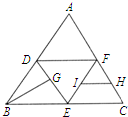 如图,在正三角形ABC中,D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将
如图,在正三角形ABC中,D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将