题目内容

数列{xn}的通项xn=（-1）n+1，前n项和为Sn，则数学公式=________．


分析：由题意可得当n为偶数时，Sn =0，=，故当n为奇数时，Sn =1，故
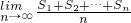=，由此求出的值．
解答：由于数列{xn}的通项xn=（-1）n+1，前n项和为Sn，
故当n为偶数时，Sn =0，故当n为奇数时，Sn =1．
∴当n为偶数时，===，
∴==．
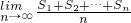当n为奇数时，===，
∴==．
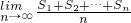故答案为：．
点评：本题主要考查求数列极限、数列求和的方法，体现了分类讨论的数学思想．
练习册系列答案
相关题目
已知函数f（x）=x2-4，设曲线y=f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1，0）（n∈N*），其中x1为正实数．
（Ⅰ）用xn表示xn+1；
（Ⅱ）若x1=4，记an=lg
xn+2xn-2
，证明数列{an}成等比数列，并求数列{xn}的通项公式；
（Ⅲ）若x1=4，bn=xn-2，Tn是数列{bn}的前n项和，证明Tn＜3．
对任意函数f（x），x∈D，可按图构造一个数列发生器．记由数列发生器产生数列{xn}．
（Ⅰ）若定义函数f(x)=
4x-2
x+1
，且输入x0=
49
65
，请写出数列{xn}的所有项；
（Ⅱ）若定义函数f（x）=2x+3，且输入x0=-1，求数列{xn}的通项公式xn．
（Ⅲ）若定义函数f（x）=xsinx（0≤x≤2π），且要产生一个无穷的常数列{xn}，试求输入的初始数据x0的值及相应数列{xn}的通项公式xn．
在xoy平面上有一系列点P1（x1，y1），P2（x2，y2），…，Pn（xn，yn），…，对每个正整数n，以点Pn为圆心的⊙Pn与x轴及射线y=
3
x，（x≥0）都相切，且⊙Pn与⊙Pn+1彼此外切．若x1=1，且xn+1＜xn（n∈N*）．
（1）求证：数列{xn}是等比数列，并求数列{xn}的通项公式；
（2）设数列{an}的各项为正，且满足an≤
xnan-1
xn+an-1
，a1=1，
求证：a1x1+a2x2+a3x3+…+anxn＜
5
4
-
1
3n-1
，（n≥2）
（3）对于（2）中的数列{an}，当n＞1时，求证：(1-an)2[
a
2
2
(1-
a
2
2
)2
+
a
3
3
(1-
a
3
3
)2
+…+
a
n
n
(1-
a
n
n
)2
]＞
4
5
-
1
1+an+
a
2
n
+…+
a
n
n
．
（2006•石景山区一模）已知函数y=f（x）对于任意θ≠
kπ2
（k∈Z），都有式子f（a-tanθ）=cotθ-1成立（其中a为常数）．
（Ⅰ）求函数y=f（x）的解析式；
（Ⅱ）利用函数y=f（x）构造一个数列，方法如下：
对于给定的定义域中的x1，令x2=f（x1），x3=f（x2），…，xn=f（xn-1），…在上述构造过程中，如果xi（i=1，2，3，…）在定义域中，那么构造数列的过程继续下去；如果xi不在定义域中，那么构造数列的过程就停止．
（ⅰ）如果可以用上述方法构造出一个常数列，求a的取值范围；
（ⅱ）是否存在一个实数a，使得取定义域中的任一值作为x1，都可用上述方法构造出一个无穷数列{xn}？若存在，求出a的值；若不存在，请说明理由；
（ⅲ）当a=1时，若x1=-1，求数列{xn}的通项公式．
精英家教网如图：已知曲线C：在点P（1，1）处的切线与x轴交于点Q1，再过Q1点作x轴的垂线交曲线C于点P1，再过P1作C的切线与x轴交于点Q2，依次重复下去，过Pn（xn，yn）作C的切线与x轴交于点Qn（xn+1，O）．
（1）求数列{xn}的通项公式；
（2）求△OPnPn+1的面积；
（3）设直线OPn的斜率为kn，求数列nkn的前n项和Sn，并证明Sn＜
79
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网