题目内容
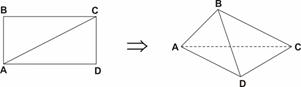
把长、宽各为4、3的长方形ABCD，沿对角线AC折成直二面角，求顶点B和顶点D的距离．分析：如图，作BE⊥AC于E，根据二面角B-AC-D为直二面角，可知BE⊥AC，进而可知BE⊥平面ADC，DE?平面ADC，BE⊥DE，在Rt△ABC中，可得BE和AE进而利用余弦定理求得cos∠EAD，进而在Rt△BDE由勾股定理求得BD．
解答：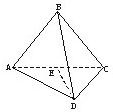
解：如图，作BE⊥AC于E，
∵二面角B-AC-D为直二面角，BE⊥AC，
∴BE⊥平面ADC，DE?平面ADC，BE⊥DE．
在Rt△ABC中，可得BE=
，AE=
，
在△ADE中，DE2=AE2+AD2-2AD•AE•
cos∠EAD=
+16-2•
•4•
=
．
在Rt△BDE中，BD2=BE2+ED2=
．
解：如图，作BE⊥AC于E，∵二面角B-AC-D为直二面角，BE⊥AC，
∴BE⊥平面ADC，DE?平面ADC，BE⊥DE．
在Rt△ABC中，可得BE=
| 12 |
| 5 |
| 9 |
| 5 |
在△ADE中，DE2=AE2+AD2-2AD•AE•
cos∠EAD=
| 81 |
| 25 |
| 9 |
| 5 |
| 4 |
| 5 |
| 193 |
| 25 |
在Rt△BDE中，BD2=BE2+ED2=
| ||
| 5 |
点评：本题主要考查了点到直线，面间的距离计算．求点到平面的距离是立体几何中较常见的一类题．一般地根据定义解题，找出这个点到面的射影，或者是找出过这个点的面的垂线段．
练习册系列答案
相关题目
