题目内容
过半径为2的球O表面上一点A作球O的截面,若OA与该截面所成的角是60°,则该截面的面积是( )A.π B.2π C.3π D.![]()
答案:A

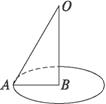
解析:如图,过A作球O的截面,其截面一定是一个小圆.
设小圆圆心为O′,
∵OO′⊥截面,
∴∠OAO′即为OA与截面所成的角.
当∠OAO′=60°时,O′A=![]() R=1.
R=1.
∴S截面=πr2=π.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
过半径为2的球O表面上一点A作球O的截面,若OA与该截面所成的角是60°则该截面的面积是( )
| A、π | ||
| B、2π | ||
C、2
| ||
| D、3π |