Question

过半径为2的球O表面上一点A作球O的截面,若OA与该截面所成的角是60°,则该截面的面积是(    )

A.π                  B.2π                   C.3π             D.π

Answer 1

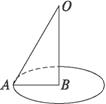
解析:过点A作截面⊙B,连结OB,AB.

∵OB⊥截面⊙B,∴∠OAB为直线OA与截面所成的角.

在Rt△OAB中,

∵OA=2,∠OAB=60°,∴AB=1.

∴截面面积S=π.

答案:A