题目内容
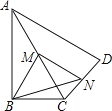
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.

(Ⅰ)证明![]() ;
;
(Ⅱ)若![]() 是
是![]() 中点,证明
中点,证明![]() 平面
平面![]() ;
;
(Ⅲ)当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() ,(Ⅰ)分别求出向量
,(Ⅰ)分别求出向量![]() 的坐标根据
的坐标根据![]() 可得结果;(Ⅱ)求出平面
可得结果;(Ⅱ)求出平面![]() 的法向量,利用向量法能证明
的法向量,利用向量法能证明![]() 平面
平面![]() ;(Ⅲ)求出平面
;(Ⅲ)求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,利用空间向量法夹角余弦公式能求出二面角
的法向量,利用空间向量法夹角余弦公式能求出二面角![]() 的余弦值.
的余弦值.
试题解析:(Ⅰ)证明:如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() .则
.则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,所以
,所以![]() .
.

(Ⅱ)解法一:

![]()
设平面![]() 的法向量
的法向量![]() ,
,
由![]()
![]() ,
,
且![]()
![]() ,
,
令![]() 得
得![]() ,
,
所以![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
解法二:证明:连接![]() ,交
,交![]() 于
于![]() ,
,![]() .
.
因为直三棱柱![]() ,
,![]() 是
是![]() 中点,
中点,
所以侧面![]() 为矩形,
为矩形,![]() 为
为![]() 的中位线.
的中位线.
所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅲ)由(Ⅰ)知![]() ,
,
设![]() ,
,
因为点![]() 在线段
在线段![]() 上,且
上,且![]() ,即
,即![]()
![]()
![]() .
.
所以![]() ,
,![]() ,
,![]()
![]() .
.
所以![]() ,
,![]() .
.
平面![]() 的法向量为
的法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由![]() ,
,![]() ,得
,得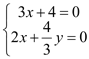 ,
,
所以![]() ,
,![]() ,
,![]()
![]() .
.
设二面角![]() 的大小为
的大小为![]() ,
,
所以 .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】“五一”假期期间,某餐厅对选择![]() 、
、![]() 、
、![]() 三种套餐的顾客进行优惠。对选择
三种套餐的顾客进行优惠。对选择![]() 、
、![]() 套餐的顾客都优惠10元,对选择
套餐的顾客都优惠10元,对选择![]() 套餐的顾客优惠20元。根据以往“五一”假期期间100名顾客对选择
套餐的顾客优惠20元。根据以往“五一”假期期间100名顾客对选择![]() 、
、![]() 、
、![]() 三种套餐的情况得到下表:
三种套餐的情况得到下表:
选择套餐种类 |
|
|
|
选择每种套餐的人数 | 50 | 25 | 25 |
将频率视为概率.
(I)若有甲、乙、丙三位顾客选择某种套餐,求三位顾客选择的套餐至少有两样不同的概率;
(II)若用随机变量![]() 表示两位顾客所得优惠金额的综合,求
表示两位顾客所得优惠金额的综合,求![]() 的分布列和期望。
的分布列和期望。