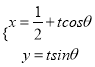题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(2)当![]() 时,若对
时,若对![]() ,
,![]() ,使得
,使得![]() 成立,求
成立,求![]() 的范围.
的范围.
【答案】(1)当![]() 时
时![]() 的最小值为
的最小值为![]() ,当
,当![]() 时
时![]() 的最小值为
的最小值为![]() ,当
,当![]() 时,
时,![]() 最小值为
最小值为![]() .(2)
.(2)![]()
【解析】试题分析:(1)本问考查利用导数求函数的最值,对函数![]() 求导数,
求导数,![]() ,令
,令![]() 得
得![]() ,对
,对![]() 分类讨论,当
分类讨论,当![]() ,
,![]() ,
,![]() 时,分别讨论函数在区间
时,分别讨论函数在区间![]() 上的单调性,从而求出函数的最小值;(2)本问主要考查“任意”、“存在”问题的等价转化,对
上的单调性,从而求出函数的最小值;(2)本问主要考查“任意”、“存在”问题的等价转化,对![]() ,
,![]() ,使得
,使得![]() 成立”等价于“
成立”等价于“![]() 在
在![]() 上的最小值不大于
上的最小值不大于![]() 在
在![]() 上的最小值”.即
上的最小值”.即![]() 由(1)问易得到函数
由(1)问易得到函数![]() 的最小值,然后通过对
的最小值,然后通过对![]() 的讨论求
的讨论求![]() 即可.
即可.
试题解析:(I)![]() ,令
,令![]() 得
得![]() .
.
当![]() 即
即![]() 时,在
时,在![]() 上
上![]() ,
,![]() 递增,
递增,![]() 的最小值为
的最小值为
![]() .
.
当![]() 即
即![]() 时,在
时,在![]() 上
上![]() ,
,![]() 为减函数,在
为减函数,在![]() 上
上![]() ,
,![]() 为增函数. ∴
为增函数. ∴![]() 的最小值为
的最小值为![]() .
.
当![]() 即
即![]() 时,在
时,在![]() 上
上![]() ,
,![]() 递减,
递减,![]() 的最小值为
的最小值为
![]() .
.
综上所述,当![]() 时
时![]() 的最小值为
的最小值为![]() ,当
,当![]() 时
时![]() 的最小值为
的最小值为![]() ,当
,当![]() 时,
时,![]() 最小值为
最小值为![]() .
.
(II)令![]()
由题可知“对![]() ,
,![]() ,使得
,使得![]() 成立”
成立”
等价于“![]() 在
在![]() 上的最小值不大于
上的最小值不大于![]() 在
在![]() 上的最小值”.
上的最小值”.
即![]()
由(I)可知,当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ,
,![]()
①当![]() 时,
时,![]()
由![]() 得
得![]() ,与
,与![]() 矛盾,舍去.
矛盾,舍去.
②当![]() 时,
时,![]()
由![]() 得
得![]() ,与
,与![]() 矛盾,舍去.
矛盾,舍去.
③当![]() 时,
时,![]()
由![]() 得
得![]()
综上,![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.