题目内容
(本小题满分12分) 已知函数 .
.
(1)求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)直线为曲线 的切线,且经过原点,求直线的方程及切点坐标.
的切线,且经过原点,求直线的方程及切点坐标.
(1) ;(2)直线的方程
;(2)直线的方程 ,切点坐标为
,切点坐标为 .
.
【解析】
试题分析:先求出 的导函数
的导函数 ,(1)由导数的几何意义,确定切线的斜率
,(1)由导数的几何意义,确定切线的斜率 ,进而由直线的点斜式即可得到所求的切线方程;(2)先设切点的坐标
,进而由直线的点斜式即可得到所求的切线方程;(2)先设切点的坐标 ,进而写出切线的方程
,进而写出切线的方程 并化简,最后根据该切线通过坐标原点,可计算出
并化简,最后根据该切线通过坐标原点,可计算出 ,进而就可写出切线的方程,确定切点的坐标.
,进而就可写出切线的方程,确定切点的坐标.
试题解析:因为 ,所以
,所以
(1)曲线 在点
在点 处的切线的斜率为
处的切线的斜率为 ,故所求切线的方程为
,故所求切线的方程为 即
即
(2)设所求切线的切点坐标为 ,则该切线的斜率为
,则该切线的斜率为
所以该切线的方程为
又因为该切线通过原点,所以
所以 ,解出
,解出
所以 ,所求的切线方程为
,所求的切线方程为 ,切点坐标为
,切点坐标为 .
.
考点:1.导数的几何意义.
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( ) B.
B. C.
C. D.
D.
 是( )
是( )
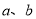 分别是方程
分别是方程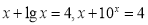 的解,
的解, 则关于
则关于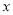 的方程
的方程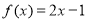 的解的个数是( )
的解的个数是( ) 的正方体的顶点都在球面上,则该球的表面积等于( )
的正方体的顶点都在球面上,则该球的表面积等于( ) B.
B. C.
C. D.
D.
 分别是定义在
分别是定义在 上的奇函数和偶函数,当
上的奇函数和偶函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 的解集是 .
的解集是 . 在点
在点 处的切线方程是( )
处的切线方程是( ) B.
B. C.
C. D.
D.
 ,
, ,则
,则 为邻边的平行四边形的面积为 .
为邻边的平行四边形的面积为 . 四所中学的学生当中随机抽取50名学生参加问卷调查,已知
四所中学的学生当中随机抽取50名学生参加问卷调查,已知 名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率; 两所中学的学生当中随机抽取两名学生,用
两所中学的学生当中随机抽取两名学生,用 表示抽得
表示抽得 中学的学生人数,求
中学的学生人数,求 的分布列及期望值.
的分布列及期望值.