题目内容
在正三棱柱ABC-A1B1C1中,若AB=
BB1,则CA1与C1B所成的角的大小是( )
| 2 |
| A、60° | B、75° |
| C、90° | D、105° |
分析:选出向量的基底,将
,
用基底表示,求出两个向量的数量积,利用向量垂直的充要条件求出两个向量的夹角.
| CA1 |
| C1B |
解答:解:设|BB1|=m,
=
,
=
,
=
则
=
+
,
=
-
•
= (
+
)•(
-
)=
2-
•
=m2-
m•
mcos
=0
∴
⊥
∴CA1与C1B所成的角的大小是90°
故选C
| C A |
| a |
| CB |
| b |
| CC1 |
| c |
| CA1 |
| a |
| c |
| C1B |
| c |
| b |
| CA1 |
| C1B |
| a |
| c |
| c |
| b |
| c |
| a |
| b |
| 2 |
| 2 |
| π |
| 3 |
∴
| CA1 |
| C1B |
∴CA1与C1B所成的角的大小是90°
故选C
点评:求两条异面直线所成的角,常利用向量作为工具,将异面直线赋予向量意义,利用向量的数量积求出两个向量所成的角,再根据异面直线所成角的范围,求出异面直线所成的角.

练习册系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.
如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.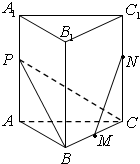 如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且
如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且 如图,在正三棱柱ABC-A'B'C'中,AB=2,若二面角C'-AB-C的大小为60°,则点C到平面ABC'的距离为
如图,在正三棱柱ABC-A'B'C'中,AB=2,若二面角C'-AB-C的大小为60°,则点C到平面ABC'的距离为