题目内容
已知集合M={-3,-2,-1,0,1,2},P(a,b)表示平面上的点(a,b∈M),问:
(1)P可表示平面上多少个不同的点?
(2)P可表示平面上多少个第二象限的点?
(3)P可表示多少个不在直线y=x上的点?
(1)36 (2)6 (3)30
解析解:(1)分两步,第一步确定a,有6种方法,第二步确定b也有6种方法,根据分步乘法计数原理共有6×6=36(个)不同的点.
(2)分两步,第一步确定a,有3种方法,第2步确定b,有2种方法,根据分步乘法计数原理,第二象限的点共有3×2=6(个).
(3)分两步,第一步确定a,有6种方法,第二步确定b,有5种方法,根据分步乘法计数原理不在直线y=x上的点共有6×5=30(个).

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
2014年某通讯公司推出一组手机卡号码,卡号的前七位数字固定,后四位数从“0000”到“9999”共10000个号码.公司规定:凡卡号的后四位带数字“5”或“8”的一律作为“金马卡”,享受一定优惠政策,则这组号码中“金马卡”的个数为( )
| A.2000 | B.4096 | C.5904 | D.8320 |
阅读图中所示的程序框图,运行相应的程序,输出的结果是 ( )
| A.123 | B.38 | C.11 | D.3 |
阅读如下程序框图,如果输出i=4,那么空白的判断框中应填入的条件是( )
| A.S<8 | B.S<9 |
| C.S<10 | D.S<11 |
 ,笔试考试成绩每次合格的概率均为
,笔试考试成绩每次合格的概率均为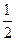 ,假设各次考试成绩合格与否均互不影响.
,假设各次考试成绩合格与否均互不影响.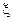 ,求参加考试次数
,求参加考试次数 空气质量进行检测,空气质量分为A、B、C三级.
空气质量进行检测,空气质量分为A、B、C三级.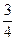 ,
,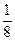 ,
, 的结果是( )
的结果是( )



