Question

（本题满分16分）本题共有3个小题，第(1)小题满分4分，第(2)小题满分5

分，第(3)小题满分7分．

将边长分别为1、2、3、…、n、n+1、…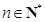（）的正方形叠放在一起，形成如图所示的图形，由小到大，依次记各阴影部分所在的图形为第1个、第2个、……、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为．记数列满足,

 

 

（1）求的表达式；

（2）写出的值，并求数列的通项公式；

（3）记，若不等式有解，求的取值范围.

 

Answer 1

【答案】

解：（1）由题意，第1个阴影部分图形的面积为，第2个阴影部分图形的面积为，……，第n个阴影部分图形的面积为.（2分）

故

                   （4分）

（2），，，

     当n为偶数时，，                        （3分）

     当n为大于1的奇数时，，

     故．                     （5分）

（3）由（2）知．

    又．

  （ⅰ）当n=1时，即，于是

（ⅱ）当n为偶数时，

即

        于是，．      （3分）

（ⅲ）当n为大于1的奇数时，

      即

于是，．        （5分）

综上所述：．                        （7分）

【解析】略