题目内容
如下图,P是边长为1的正六边形ABCDEF所在平面外一点,PA=1,P在平面ABC内的射影为BF的中点O.
(1)证明PA⊥BF;
(2)求面APB与面DPB所成二面角的大小.
解法1:连结AD,则易知AD与BF的交点为O.

(1)证法1:∵AB=AF,O为BF的中点,∴AO⊥BF
又∵PO⊥平面ABC,
∴由三垂线定理得PA⊥BF
证法2:∵BF⊥PO,BF⊥AO,PO∩AO=O,∴BF⊥平面AOP.
∵PA![]() 平面AOP,∴PA⊥BF.
平面AOP,∴PA⊥BF.
(2)解:设M为PB的中点,连结AM、MD.
∵在△ABP中PA=AB,∴PB⊥AM.
∵斜线PB在平面ABC内的射影为OB,BF⊥AD,∴由三垂线定理得PB⊥AD.
又∵AM∩AD=A,∴PB⊥平面AMD.
∵MD![]() 平面AMD,∴PB⊥MD.
平面AMD,∴PB⊥MD.
因此∠AMD为所求二面角的平面角.
在正六边形ABCDEF中,BD=BF=2OB=![]() ,AD=2.
,AD=2.
在Rt△AOP中,PA=1,OA=![]() ∴PO=
∴PO=![]()
在Rt△BOP中,PB=![]() ,则
,则
BM=C,AM=![]() ,MD=
,MD=![]() .
.
在△AMD中,由余弦定理得cosAMD=![]() .
.
因此,所求二面角的大小为arccos(-![]() ).
).
解法2:?由题设条件,以O为原点建立空间直角坐标系O-xyz.如图,由正六边形的性质,可得OA=![]() ,OB=OF=
,OB=OF=![]() ,OD=
,OD=![]()
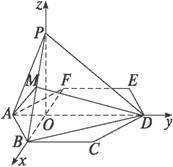
在Rt△AOP中,PA=1,OA=![]() ,故OP=
,故OP=![]() .
.
因而有A(0,-![]() ,0),B(
,0),B(![]() ,0,0),D(0,
,0,0),D(0,![]() ,0),F(-
,0),F(-![]() ,0,0),P(0,0,
,0,0),P(0,0,![]() ).
).
(1)证明:因![]() =(0,-
=(0,-![]() ,-
,-![]() ),
), ![]() =(-
=(-![]() ,0,0),故
,0,0),故![]()
![]()
![]() =0.所以PA⊥BF.
=0.所以PA⊥BF.
(2)解:设M为PB的中点,连结AM、MD,则M点的坐标为(![]() ).
).
∵![]() =
=![]() =0,
=0,
![]() =(
=(![]() =0,
=0,
∴MA⊥PB,MD⊥PB.
因此,∠AMD为所求二面角的平面角.
∵![]() =
=![]() ,
,![]() ,
,
![]() ,
,
∴cos<![]() >=
>=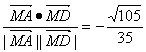
因此,所求二面角的大小为arccos(![]() ).
).

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
(2006
安微,19)如下图,P是边长为1的正六边形ABCDEF所在平面外一点,PA=1,P在平面ABC内的射影为BF的中点O.(1)
证明:PA⊥BF;(2)
求面APB与面DPB所成二面角的大小.
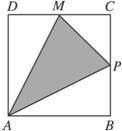
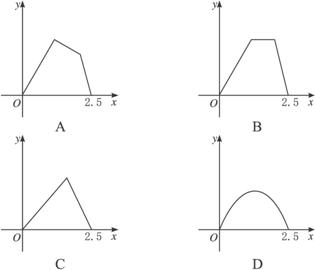
 如图,点P在边长为1的正方形ABCD上运动,设点M为CD的中点,当点P沿A→B→C→M运动时,点P经过的路程设为x,△APM面积设为y,则函数y=f(x)的图象只可能是下图中的( )
如图,点P在边长为1的正方形ABCD上运动,设点M为CD的中点,当点P沿A→B→C→M运动时,点P经过的路程设为x,△APM面积设为y,则函数y=f(x)的图象只可能是下图中的( )