题目内容
(2006
安微,19)如下图,P是边长为1的正六边形ABCDEF所在平面外一点,PA=1,P在平面ABC内的射影为BF的中点O.(1)
证明:PA⊥BF;(2)
求面APB与面DPB所成二面角的大小.
答案:略
解析:
解析:
|
解析:连结 AD,则易知AD与BF的中点为O.(1) 证法一:∵AB=AF,O为BF的中点,
∴ AO⊥BF.又∵ PO⊥平面ABC,∴由三垂线定理得 PA⊥BF.证法二:∵ BF⊥PO,BF⊥AO,PO∩AO=O,∴ BF⊥平面AOP.∵ PA 平面AOP,∴PA⊥BF. 平面AOP,∴PA⊥BF.
(2) 设M为PB的中点,连结AM,MD.∵在△ ABP中PA=AB,∴PB⊥AM.∵斜线 PB在平面ABC内的射影为OB,BF⊥AD,∴由三垂线定理得 PB⊥AD.又∵ AM∩AD=A,∴PB⊥平面AMD.∵ MD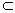 平面AMD,∴PB⊥MD. 平面AMD,∴PB⊥MD.
因此,∠ AMD为所求二面角的平面角.在正六边形 ABCDEF中,
在 Rt△AOP中,PA=1,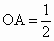 , ,
∴ 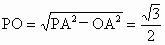 . .
在 Rt△BOP中,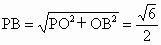 , ,
则 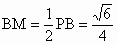 , ,
在△ AMD中,由余弦定量得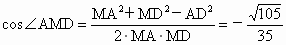 . .
因此,所求二面角的大小为 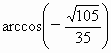 . . |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



