题目内容
如图，正方体ABCD-A1B1C1D1中，E为棱AB的中点，则直线C1E与平面ACC1A1所成角的正切值为 ．
【答案】分析：以A为坐标原点，AB，AD，AA1分别为x，y，z轴正方向，建立空间坐标系O-xyz，分别求出面ACC1A1的法向量和直线C1E的方向向量，代入向量夹角公式，可得C1E与平面ACC1A1所成角的正弦值，进而根据同角三角函数关系求出正切值．
解答：解：以A为坐标原点，AB，AD，AA1分别为x，y，z轴正方向，建立空间坐标系O-xyz
设正方体ABCD-A1B1C1D1的棱长为2
则A（0，0，0），B（2，0，0），D（0，2，0），E（1，0，0），C1（2，2，2）
根据正方体的几何特征，可得BD⊥平面ACC1A1，
故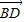
=（-2，2，0）是平面ACC1A1的一个法向量
又∵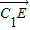
=（-1，-2，-2）
故C1E与平面ACC1A1所成角θ满足sinθ=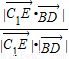
=
=
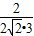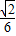
则cosθ=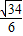
，tanθ=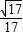
故答案为：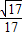
点评：本题考查的知识点是直线与平面所成的角，其中建立空间坐标系，将线面夹角问题转化为向量夹角问题是解答的关键．
解答：解：以A为坐标原点，AB，AD，AA1分别为x，y，z轴正方向，建立空间坐标系O-xyz
设正方体ABCD-A1B1C1D1的棱长为2
则A（0，0，0），B（2，0，0），D（0，2，0），E（1，0，0），C1（2，2，2）
根据正方体的几何特征，可得BD⊥平面ACC1A1，
故
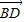=（-2，2，0）是平面ACC1A1的一个法向量又∵
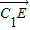=（-1，-2，-2）故C1E与平面ACC1A1所成角θ满足sinθ=
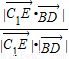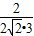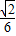
==则cosθ=
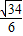，tanθ=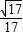故答案为：
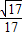
点评：本题考查的知识点是直线与平面所成的角，其中建立空间坐标系，将线面夹角问题转化为向量夹角问题是解答的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，正方体ABCD-A1B1C1D1中，E，F分别为BB1和A1D1的中点．证明：向量
如图，正方体ABCD-A1B1C1D1棱长为8，E、F分别为AD1，CD1中点，G、H分别为棱DA，DC上动点，且EH⊥FG．
如图，正方体ABCD-A1B1C1D1中，若E、F、G分别为棱BC、C1C、B1C1的中点，O1、O2分别为四边形ADD1A1、A1B1C1D1的中心，则下列各组中的四个点不在同一个平面上的是（ ）
如图，正方体ABCD-A1B1C1D1中，E、F、G、H分别是所在棱的三等分点，且