题目内容
10.某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获得利润分别为4万元、3万元,则该企业每天可获得最大利润为13万元| 甲 | 乙 | 原料限额 | |
| A(吨) | 2 | 5 | 10 |
| B(吨) | 6 | 3 | 18 |
分析 设每天生产甲乙两种产品分别为x,y吨,利润为z元,然后根据题目条件建立约束条件,得到目标函数,画出约束条件所表示的区域,然后利用平移法求出z的最大值.
解答 解:设每天生产甲乙两种产品分别为x,y吨,利润为z元,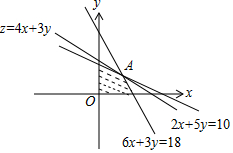
则$\left\{\begin{array}{l}{2x+5y≤10}\\{6x+3y≤18}\\{x≥0,y≥0}\end{array}\right.$,
目标函数为 z=4x+3y.
作出二元一次不等式组所表示的平面区域(阴影部分)即可行域.
由z=4x+3y得y=-$\frac{4}{3}x+\frac{z}{3}$,
平移直线y=-$\frac{4}{3}$x+$\frac{z}{3}$,由图象可知当直线y=-$\frac{4}{3}$x+$\frac{z}{3}$经过点A时,直线的截距最大,
此时z最大,
解方程组$\left\{\begin{array}{l}{2x+5y=10}\\{6x+3y=18}\end{array}\right.$,解得:A($\frac{5}{2},1$),
∴zmax=4x+3y=10+3=13.
则每天生产甲乙两种产品分别为2.5,1吨,能够产生最大的利润,最大的利润是13万元.
故答案为:13.
点评 此题考查了线性规划的应用,建立约束条件和目标函数,利用数形结合是解本题的关键,是中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
20.已知函数f(x)=ex-ax有两个零点x1,x2,x1<x2,则下面说法正确的是( )
| A. | x1+x2<2 | B. | a<e | ||
| C. | x1x2>1 | D. | 有极小值点x0,且x1+x2<2x0 |
5.若实数x,y满足约束条件$\left\{\begin{array}{l}{x-1≥1}\\{x-y≤0}\\{x+y-6≤0}\end{array}\right.$,则z=2x+y的最大值为( )
| A. | 9 | B. | 4 | C. | 6 | D. | 3 |
15.在平面直角坐标系中,若角α的顶点与原点重合,始边与x轴的非负半轴重合,终边过点P(-$\sqrt{3}$,-1),则sin($\frac{π}{2}$-α)=( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
20.已知向量$\overrightarrow a$与$\overrightarrow b$的夹角为${60°},|{\overrightarrow a}|=2,|{\overrightarrow b}|=5$,则|$2\overrightarrow a-\overrightarrow b$|的值为( )
| A. | 21 | B. | $\sqrt{21}$ | C. | $\sqrt{23}$ | D. | $\sqrt{35}$ |
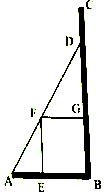 如图欲在直角区域ABC内的空地上植造一块“绿地Rt△ABD”,D在BC边上.其中AB=1,设BD=x(x>0)且BC足够长,规划在△ABD的内接正方形BEFG内种花,其余地方种草,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“完美度”.
如图欲在直角区域ABC内的空地上植造一块“绿地Rt△ABD”,D在BC边上.其中AB=1,设BD=x(x>0)且BC足够长,规划在△ABD的内接正方形BEFG内种花,其余地方种草,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“完美度”.