题目内容
已知函数f(x)=x3+ax2+bx+c,f(x)在点x=0处取得极值,并且在单调区间[0,3]和[5,6]上具有相反的单调性.(1)求实数b的值;
(2)求实数a的取值范围.
【答案】分析:(1)f′(x)=3x2+2ax+b,由f(x)在点x=0处取得极值,可得f′(0)=0,解得b=0.
可得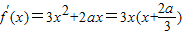 .利用取得
.利用取得
可知a≠0时,b=0时,利用取得极值的条件即可得出.
(2)由于f(x)在单调区间[0,3]和[5,6]上具有相反的单调性.
可知:f′(x)区间[0,3]和[5,6]上具有相反的符号.分为以下两种情况:
1°若f′(x)区间[0,3]上f′(x)>0,则[5,6]上f′(x)<0.
2°若f′(x)区间[0,3]上f′(x)<0,则[5,6]上f′(x)>0.对a分类讨论即可.
解答:解:(1)f′(x)=3x2+2ax+b,∵f(x)在点x=0处取得极值,∴f′(0)=0,解得b=0.
∴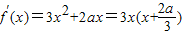 .
.
可知a≠0时,b=0时,f′(x)在x=0处的左右符号相反,因此函数f(x)在点x=0处取得极值.
(2)由(1)可知: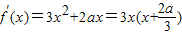 =
=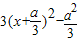 .
.
∵f(x)在单调区间[0,3]和[5,6]上具有相反的单调性.
∴f′(x)区间[0,3]和[5,6]上具有相反的符号.分为以下两种情况:
1°若f′(x)区间[0,3]上f′(x)>0,则[5,6]上f′(x)<0.
2°若f′(x)区间[0,3]上f′(x)<0,则[5,6]上f′(x)>0.
①当a>0时,f′(x)在区间[0,+∞)单调递增,∴f′(3)≤0,且f′(5)≥0,解得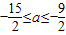 ,应舍去;
,应舍去;
②当a<0时,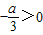 .f′(x)在区间[0,
.f′(x)在区间[0,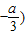 单调递减,在区间
单调递减,在区间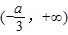 单调递增.
单调递增.
∵f′(0)=0,∴必有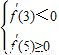 ,解得
,解得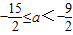 .
.
综上可知:实数a的取值范围是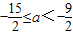 .
.
点评:熟练掌握利用导数研究函数取得极值的条件、单调性、二次函数的单调性是解题的关键.
可得
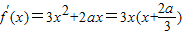 .利用取得
.利用取得可知a≠0时,b=0时,利用取得极值的条件即可得出.
(2)由于f(x)在单调区间[0,3]和[5,6]上具有相反的单调性.
可知:f′(x)区间[0,3]和[5,6]上具有相反的符号.分为以下两种情况:
1°若f′(x)区间[0,3]上f′(x)>0,则[5,6]上f′(x)<0.
2°若f′(x)区间[0,3]上f′(x)<0,则[5,6]上f′(x)>0.对a分类讨论即可.
解答:解:(1)f′(x)=3x2+2ax+b,∵f(x)在点x=0处取得极值,∴f′(0)=0,解得b=0.
∴
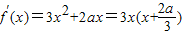 .
.可知a≠0时,b=0时,f′(x)在x=0处的左右符号相反,因此函数f(x)在点x=0处取得极值.
(2)由(1)可知:
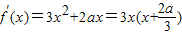 =
=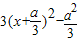 .
.∵f(x)在单调区间[0,3]和[5,6]上具有相反的单调性.
∴f′(x)区间[0,3]和[5,6]上具有相反的符号.分为以下两种情况:
1°若f′(x)区间[0,3]上f′(x)>0,则[5,6]上f′(x)<0.
2°若f′(x)区间[0,3]上f′(x)<0,则[5,6]上f′(x)>0.
①当a>0时,f′(x)在区间[0,+∞)单调递增,∴f′(3)≤0,且f′(5)≥0,解得
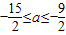 ,应舍去;
,应舍去;②当a<0时,
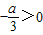 .f′(x)在区间[0,
.f′(x)在区间[0,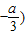 单调递减,在区间
单调递减,在区间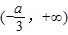 单调递增.
单调递增.∵f′(0)=0,∴必有
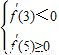 ,解得
,解得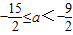 .
.综上可知:实数a的取值范围是
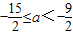 .
.点评:熟练掌握利用导数研究函数取得极值的条件、单调性、二次函数的单调性是解题的关键.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|