题目内容
8.在△ABC中,E为AC上一点,且$\overrightarrow{AC}=4\overrightarrow{AE}$,P为BE上一点,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$(m>0,n>0),则$\frac{1}{m}$+$\frac{1}{n}$的最小值是9.分析 $\overrightarrow{AC}=4\overrightarrow{AE}$,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$(m>0,n>0),可得 $\overrightarrow{AP}=m\overrightarrow{AB}+4n\overrightarrow{AE}$.由向量共线定理可得:m+4n=1.再利用“乘1法”与基本不等式的性质即可得出.
解答 解:∵$\overrightarrow{AC}=4\overrightarrow{AE}$,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$(m>0,n>0),
∴$\overrightarrow{AP}=m\overrightarrow{AB}+4n\overrightarrow{AE}$.
∵P为BE上一点,
由向量共线定理可得:m+4n=1.
∴$\frac{1}{m}$+$\frac{1}{n}$=(m+4n)($\frac{1}{m}$+$\frac{1}{n}$)=5+$\frac{4n}{m}+\frac{m}{n}$$≥5+2\sqrt{\frac{4n}{m}•\frac{m}{n}}$=9,当且仅当m=2n=$\frac{1}{3}$时取等号.
∴$\frac{1}{m}$+$\frac{1}{n}$的最小值是9.
故答案为:9.
点评 本题考查了向量共线定理、“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
1.已知向量$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(3,0),若(2$\overrightarrow{a}$+$\overrightarrow{b}$)∥(m$\overrightarrow{a}$-$\overrightarrow{b}$),则m的值为( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
16.已知集合M={x∈R|x2-x=0},N={x|x=2n+1,n∈Z},则M∩N为( )
| A. | {0} | B. | {0,1} | C. | {1} | D. | ∅ |
3.把函数y=2sinx图象上各点的横坐标缩短为原来的$\frac{1}{2}$,然后把所得的图象再向右平移$\frac{π}{6}$个单位,则所得图象对应的函数解析式为( )
| A. | y=2sin($\frac{1}{2}x+\frac{π}{6}$) | B. | y=2sin(2x-$\frac{π}{3}$) | C. | y=sin($\frac{1}{2}x-\frac{π}{3}$) | D. | y=2sin(2x+$\frac{π}{3}$) |
19.已知f(x)是定义在R上的函数,且满足f(-x)=f(x),f(x+2)=f(2-x).若曲线y=f(x)在x=-1处的切线方程为x-y+3=0,则该曲线在x=5处的切线方程为( )
| A. | x-y-3=0 | B. | x-y-7=0 | C. | x+y-3=0 | D. | x+y-7=0 |
 .
. 中,已知
中,已知 ,点
,点 和点
和点 分别在线段
分别在线段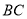 和
和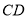 上,且
上,且 ,则
,则 的值为_____________.
的值为_____________.