题目内容

已知
OA 
=
a 
，
OB 
=
b 
，且|
a 
| = |
b 
| =4，∠AOB=60°，
（1）求|
a 
+
b 
|，|
a 
-
b 
|；
（2）求（
a 
+
b 
）与
a 
的夹角．
分析：（1）由题意可得：
a 
 • 
b 
= |
a 
|  | 
b 
|cos＜
a 
 ，  
b 
＞ =16cos60°=8，再结合求模公式|
a
|=
(
a
)2
可得答案．
（2）设( 
a 
 + 
b 
 ) 与 
a 
的夹角为θ，由向量的数量积公式变形可得：cosθ=
(
a
+
b
)  • 
a
|
a
+
b
|  • |
a
|
，再结合题中的条件与（1）的结论可得答案．
解答：解：（1）因为|
a 
| = |
b 
| =4，∠AOB=60°，
所以
a 
 • 
b 
= |
a 
|  | 
b 
|cos＜
a 
 ，  
b 
＞ =16cos60°=8，
所以|
a 
 + 
b 
| =
|
a 
 |2+2 
a 
 • 
b 
+|
b 
 |2
=
16×2+16
=4
3
，|
a 
 - 
b 
| =
|
a 
 |2-2 
a 
 • 
b 
+|
b 
 |2
=
16-16+16
=4（7分）
（2）设( 
a 
 + 
b 
 ) 与 
a 
的夹角为θ
所以cosθ=
( 
a 
 + 
b 
 )  •  
a 
| 
a 
 + 
b 
|  • | 
a 
|
=
|
a 
|2+ 
a 
 • 
b 
| 
a 
 + 
b 
|  • | 
a 
|
=
16+8
4
3
•4
=
3
2
3
=
3
2

所以θ=
π
6
，即（
a 
+
b 
）与
a 
的夹角为
π
6
．（13分）
点评：解决此类问题的关键是熟练掌握向量的数量积公式及其应用，以及熟练掌握求模公式|
a
|=
(
a
)2
，此题属于基础题．
练习册系列答案
相关题目
已知点A（1，0），B（0，1），C（2sinθ，cosθ）．
（1）若|
AC
|=|
BC
|，求tanθ的值；
（2）若(
OA
+2
OB
)•
OC
=1，其中O为坐标原点，求sin2θ的值
（2013•蓟县二模）已知点A，B，C在圆x2+y2=1，满足2
OA
+
AB
+
AC
=
0
（其中O为坐标原点），又|
AB
|=|
OA
|，则向量
BA
在向量
BC
方向上的投影为（　　）
已知点A、O、B为平面内不共线的三点，若Ai（i=1，2，3，…，n）是该平面内的任一点，且有
OAi
•
OB
=
OA
•
OB
，则点Ai（i=1，2，3，…，n）在（　　）
A、过A点的抛物线上
B、过A点的直线上
C、过A点的圆心的圆上
D、过A点的椭圆上

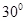已知OA是球O的半径，过点A作与直线OA成30°的平面截球面得到圆M，若圆M的面积为12π，则球O的表面积是________．

已知OA是球O的半径，过点A作与直线OA成的平面截球面得到圆M，若圆M的面积为15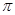，则球O的表面积是                 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网