题目内容
点P是双曲线C1:
解析:a2+b2=c2,圆C2过两个焦点,∠F1PF2=90°,∠PF1F2=30°,∠PF2F1=60°,设|PF1|=r1,|PF2|=r2,则在△PF1F2中,![]() 而r1-r2=2a,则
而r1-r2=2a,则![]()
答案:![]() +1
+1

练习册系列答案
相关题目
点P是双曲线C1:
-
=1(a>0,b>0)与圆C2:x2+y2=a2+b2的一个交点,且2∠PF1F2=∠PF2F1,其中F1、F2分别为双曲线C1的左右焦点,则双曲线C1的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
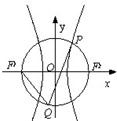 如图,点P是双曲线C1:
如图,点P是双曲线C1: 和圆C2:x2+y2=a2+b2的一个交点,Q是圆C2在x轴下方的一点,且∠F1QP=60o,其中F1、F2是双曲线C1的两个焦点,则双曲线C1的离心率为 .
和圆C2:x2+y2=a2+b2的一个交点,Q是圆C2在x轴下方的一点,且∠F1QP=60o,其中F1、F2是双曲线C1的两个焦点,则双曲线C1的离心率为 .