题目内容
5.已知双曲线$C:\frac{x^2}{4}-\frac{y^2}{3}=1$,其右顶点为P.(1)求以P为圆心,且与双曲线C的两条渐近线都相切的圆的标准方程;
(2)设直线l过点P,其法向量为$\overrightarrow{n}$=(1,-1),若在双曲线C上恰有三个点P1,P2,P3到直线l的距离均为d,求d的值.
分析 (1)利用点到直线的距离公式,求出圆的半径,即可求出圆的标准方程;
(2)求出与直线l平行,且与双曲线消去的直线方程,即可得出结论.
解答 解:(1)由题意,P(2,0),双曲线的渐近线方程为y=±$\frac{\sqrt{3}}{2}$x,P到渐近线的距离d=$\frac{\sqrt{3}}{\sqrt{\frac{3}{4}+1}}$=$\sqrt{\frac{12}{7}}$,
∴圆的标准方程为(x-2)2+y2=$\frac{12}{7}$;
(2)由题意,直线l的斜率为1,设与直线l平行的直线方程为y=x+m,代入双曲线方程整理可得x2+8mx+4m2+12=0,△=64m2-4(4m2+12)=0,可得m=±1,
与直线l:y=x+2的距离分别为$\frac{1}{\sqrt{2}}$或$\frac{3}{\sqrt{2}}$,即d=$\frac{\sqrt{2}}{2}$或$\frac{3\sqrt{2}}{2}$
点评 本题考查双曲线的方程与性质,考查圆的方程,考查直线与双曲线位置关系的运用,属于中档题.

练习册系列答案
相关题目
13.已知△AOB中,∠AOB=120°,|$\overrightarrow{OA}$|=3,|$\overrightarrow{OB}$|=2,过O作OD垂直AB于点D,点E为线段OD的中点,则$\overrightarrow{OE}$•$\overrightarrow{EA}$的值为( )
| A. | $\frac{5}{19}$ | B. | $\frac{27}{76}$ | C. | $\frac{3}{76}$ | D. | $\frac{3}{19}$ |
20.利用反证法证明:“若x2+y2=0,则x=y=0”时,假设为( )
| A. | x,y都不为0 | B. | x≠y且x,y都不为0 | C. | x≠y且x,y不都为0 | D. | x,y不都为0 |
14.在数列{an}中,已知a1=0,an+2-an=2,则a7的值为( )
| A. | 9 | B. | 15 | C. | 6 | D. | 8 |
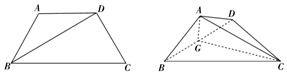 如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上.
如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上.