题目内容
设函数
，且曲线
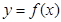斜率最小的切线与直线
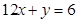平行.求：（1）
的值；(2）函数
的单调区间.
（1）
(2）增区间是
和
，减区间是（-1，3）
解析试题分析：（1）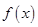
的定义域为R
所以
，
由条件得
，解得或
（舍）
所以
(2）因为，所以
，
，解得
或
所以当
或
时，
当
时，
，
所以的单调增区间是和，减区间是（-1，3）.
考点：导数的几何意义及函数单调区间
点评：利用导数的几何意义可求出函数在某一点出的切线斜率，求增区间需解不等式，求减区间需解不等式
练习册系列答案
名校课堂系列答案
相关题目
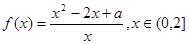，其中常数a > 0．
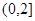上是减函数；
，
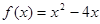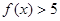，求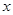
的范围； （2）不等式
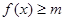对任意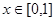
恒成立，求实数
的取值范围。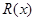
万元，且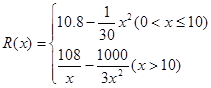
．
（万元）关于年产品（千件）的函数解析式；
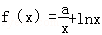，g（x）=
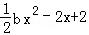，a，b∈R．
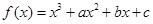,曲线
在点
处的切线为
，若
时，
的值；
上的最大值和最小值.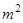
的矩形蔬菜温室。在温室内，沿左．右两侧与后侧内墙各保留1
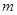宽的通道，沿前侧内墙保留3 
的有铝合金盖的圆柱形铁桶，已知单位面积铝合金的价格是铁的3倍，问底面半径多大时桶的总造价最小？