题目内容
盒子中装有大小相同的2只红球,4只黑球,n(n≥3)只白球.规定:一次摸出3只球,如果这3只球是同色的,就奖励10元,否则罚款2元.某人摸一次球,他获奖励10元的概率为p.
(1)当n=4时,
(i)若某人摸一次球,求他获奖励10元的概率;
(ii)若有10人参加摸球游戏,每人摸一次,摸后放回,记随机变量ξ为获奖励的人数.求P(ξ>1),和这10人所得总钱数的期望.(结果用分数表示,参考数据:(
)10≈
)
(2)记某人三次摸球恰有一次中奖10元的概率为f(p),问当n为何值时,f(p)取得最大值.
(1)当n=4时,
(i)若某人摸一次球,求他获奖励10元的概率;
(ii)若有10人参加摸球游戏,每人摸一次,摸后放回,记随机变量ξ为获奖励的人数.求P(ξ>1),和这10人所得总钱数的期望.(结果用分数表示,参考数据:(
| 14 |
| 15 |
| 1 |
| 2 |
(2)记某人三次摸球恰有一次中奖10元的概率为f(p),问当n为何值时,f(p)取得最大值.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)(i)某人摸一次球,利用古典概型概率计算公式能求出他获奖励10元的概率.
(ii)由题意知ξ~B(10,
),由此能求出P(ξ>1)和这10人所得总钱数的期望.
(2)三次摸球恰有一次中奖10元的概率为f(p)=
p(1-p)2=3p3-6p2+3p,0<p<1,由此能求出当n=14时,f(p)取最大值.
(ii)由题意知ξ~B(10,
| 1 |
| 15 |
(2)三次摸球恰有一次中奖10元的概率为f(p)=
| C | 1 3 |
解答:
(本小题满分14分)
解:(1)(i)某人摸一次球,他获奖励10元的概率:
p=
=
.
(ii)由题意知ξ~B(10,
),
则P(ξ>1)=1-P(ξ=0)-P(ξ=1)
=1-(
)10-
×
×(
)9
=
.
设η为在一局中的输赢,则Eη=
×10-
×2=-
,
∴E(10η)=10Eη=10×(-
)=-12.
(2)摸一次球中奖10元的概率为p=
(n≥3)
三次摸球恰有一次中奖10元的概率为:
f(p)=
p(1-p)2=3p3-6p2+3p,0<p<1,
f'(p)=9p2-12p+3=3(p-1)(3p-1),0<p<1
∴f(p)在(0,
)是增函数,在(
,1)是减函数,
将n=3,4,5…分别代入p=
知:
当3≤n≤13时,p的值递增,
且当n=13时,p=
=0.299,
f(0.299)=
0.299×(1-0.299)2=0.441
当n=14时,p=
=0.323,
f(0.323)=
0.323×(1-0.323)2=0.444
所以当n=14时,f(p)取最大值.…(14分)
解:(1)(i)某人摸一次球,他获奖励10元的概率:
p=
2
| ||
|
| 1 |
| 15 |
(ii)由题意知ξ~B(10,
| 1 |
| 15 |
则P(ξ>1)=1-P(ξ=0)-P(ξ=1)
=1-(
| 14 |
| 15 |
| C | 1 10 |
| 1 |
| 15 |
| 14 |
| 15 |
=
| 1 |
| 7 |
设η为在一局中的输赢,则Eη=
| 1 |
| 15 |
| 14 |
| 15 |
| 6 |
| 5 |
∴E(10η)=10Eη=10×(-
| 6 |
| 5 |
(2)摸一次球中奖10元的概率为p=
| ||||
|
三次摸球恰有一次中奖10元的概率为:
f(p)=
| C | 1 3 |
f'(p)=9p2-12p+3=3(p-1)(3p-1),0<p<1
∴f(p)在(0,
| 1 |
| 3 |
| 1 |
| 3 |
将n=3,4,5…分别代入p=
| ||||
|
当3≤n≤13时,p的值递增,
且当n=13时,p=
| ||||
|
f(0.299)=
| C | 1 3 |
当n=14时,p=
| ||||
|
f(0.323)=
| C | 1 3 |
所以当n=14时,f(p)取最大值.…(14分)
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
命题“若α=
,则sinα=1”的逆否命题是( )
| π |
| 2 |
A、若α≠
| ||
B、若α=
| ||
C、若sinα≠1,则α≠
| ||
D、若sinα≠1,则α=
|
 表示实心圆,
表示实心圆, 表示空心圆):
表示空心圆):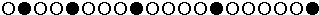
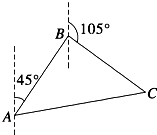 如图所示,我艇在A处发现一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃窜,我艇立即以14海里/小时的速度追击,求我艇追上走私船所需要的最短时间.
如图所示,我艇在A处发现一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃窜,我艇立即以14海里/小时的速度追击,求我艇追上走私船所需要的最短时间.