题目内容
有下列4个命题(1)第一象限角是锐角;
(2)y=sin(
| π |
| 4 |
| 3 |
| 8 |
| 7 |
| 8 |
(3)角α终边经过点(a,a)(a≠0)时,sinα+cosα=
| 2 |
(4)若y=
| 1 |
| 2 |
| 1 |
| 2 |
其中正确命题为
分析:找特殊角α=370°即可判断(1);先将y=sin(
-2x)根据诱导公式进行化简,再由正弦函数的单调性可求其单调增区间,进而判断(2)正确;当角α终边经过点(a,a)(a≠0)时,对a的正负分两种情况进行讨论,进而可求得sinα+cosα=
或-
,进而(3)不对;根据正弦函数的最小正周期的求法可T=
,进而可求出ω的值,得到(4)正确.
| π |
| 4 |
| 2 |
| 2 |
| 2π |
| ω |
解答:解:α=370°是第一象限角,但不是锐角,故(1)不对;
∵y=sin(
-2x)=-sin(2x-
),令
+2kπ≤2x-
≤
+2kπ
∴
+kπ≤x≤
+kπ∴y=sin(
-2x)的单调增区间是(kπ+
π,kπ+
π),k∈Z;故(2)正确;
∵角α终边经过点(a,a)(a≠0)时,当a>0时,sinα=
,cosα=
,
当a<0时,sinα=-
,cosα=-
,
∴sinα+cosα=
或-
,故(3)不对;
∵y=
sin(ωx)的最小正周期为4π∴T=
=4π,∴ω=
,故(4)正确.
故答案为:(2),(4).
∵y=sin(
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
∴
| 3π |
| 8 |
| 7π |
| 8 |
| π |
| 4 |
| 3 |
| 8 |
| 7 |
| 8 |
∵角α终边经过点(a,a)(a≠0)时,当a>0时,sinα=
| ||
| 2 |
| ||
| 2 |
当a<0时,sinα=-
| ||
| 2 |
| ||
| 2 |
∴sinα+cosα=
| 2 |
| 2 |
∵y=
| 1 |
| 2 |
| 2π |
| ω |
| 1 |
| 2 |
故答案为:(2),(4).
点评:本题主要考查三角函数的基本内容--象限角、正余弦函数值、正弦函数的最小正周期和单调性.高考对三角函数的考查以基础为主,一定要强化基础的夯实.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 -2x)的单调增区间是(
-2x)的单调增区间是(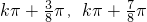 ),k∈Z;
),k∈Z; ;
; sin(ωx)的最小正周期为4π,则ω=
sin(ωx)的最小正周期为4π,则ω=