题目内容
已知数列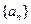 中,
中,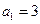 ,
,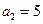 ,其前
,其前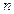 项和
项和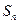 满足
满足
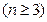 ,令
,令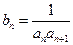 .
.
(Ⅰ)求数列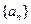 的通项公式;
的通项公式;
(Ⅱ)令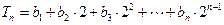 ,求证:
,求证:
① 对于任意正整数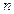 ,都有
,都有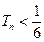 ;
;
② 对于任意的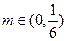 ,均存在
,均存在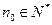 ,使得
,使得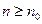 时,
时,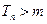 .
.

解析解:(Ⅰ) 由题意知 即
即



检验知 时,结论也成立故
时,结论也成立故 .
.
① 由于



② 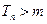 ,其中
,其中 ,则有
,则有 ,则
,则 ,
,
故 ,
,
取
(其中 表示不超过
表示不超过 的最大整数),则当
的最大整数),则当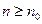 时,
时,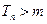 .
.

练习册系列答案
相关题目
题目内容
已知数列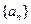 中,
中,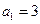 ,
,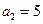 ,其前
,其前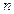 项和
项和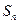 满足
满足
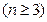 ,令
,令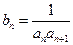 .
.
(Ⅰ)求数列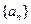 的通项公式;
的通项公式;
(Ⅱ)令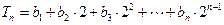 ,求证:
,求证:
① 对于任意正整数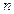 ,都有
,都有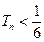 ;
;
② 对于任意的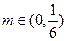 ,均存在
,均存在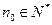 ,使得
,使得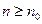 时,
时,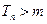 .
.

解析解:(Ⅰ) 由题意知 即
即



检验知 时,结论也成立故
时,结论也成立故 .
.
① 由于



② 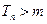 ,其中
,其中 ,则有
,则有 ,则
,则 ,
,
故 ,
,
取
(其中 表示不超过
表示不超过 的最大整数),则当
的最大整数),则当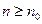 时,
时,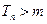 .
.
