题目内容
已知甲箱中只放有x个红球与y个白球(x,y≥0且x+y=6),乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别).若甲箱从中任取2个球,从乙箱中任取1个球.
(Ⅰ)记取出的3个球的颜色全不相同的概率为P,求当P取得最大值时x,y的值;
(Ⅱ)当x=2时,求取出的3个球中红球个数ξ的期望E(ξ).
(Ⅰ)记取出的3个球的颜色全不相同的概率为P,求当P取得最大值时x,y的值;
(Ⅱ)当x=2时,求取出的3个球中红球个数ξ的期望E(ξ).
(I)由题意知:
P=
=
≤
(
)2=
,
当且仅当x=y时,取等号,故当P取得最大值时x,y的值都为3.
(II)当x=2时,即甲箱中有2个红球与4个白球,故ξ的取值是0,1,2,3.
则P(ξ=0)=
=
;P(ξ=1)=
=
;
P(ξ=2)=
=
;P(ξ=3)=
=
;
所以ξ的分布列为(必须写出分布列,否则扣1分)
…(11分)
故Eξ=0×
+1×
+2×
+3×
=
,
所求取出的3个球中红球个数ξ的期望E(ξ)=
.
P=
| ||||
|
| xy |
| 60 |
| 1 |
| 60 |
| x+y |
| 2 |
| 3 |
| 20 |
当且仅当x=y时,取等号,故当P取得最大值时x,y的值都为3.
(II)当x=2时,即甲箱中有2个红球与4个白球,故ξ的取值是0,1,2,3.
则P(ξ=0)=
| ||||
|
| 1 |
| 5 |
| ||||||||||
|
| 7 |
| 15 |
P(ξ=2)=
| ||||||||||
|
| 3 |
| 10 |
| ||||
|
| 1 |
| 30 |
所以ξ的分布列为(必须写出分布列,否则扣1分)
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
故Eξ=0×
| 1 |
| 5 |
| 7 |
| 15 |
| 3 |
| 10 |
| 1 |
| 30 |
| 7 |
| 6 |
所求取出的3个球中红球个数ξ的期望E(ξ)=
| 7 |
| 6 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 且
且 ,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.
,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.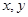 的值;
的值;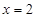 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数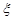 的期望
的期望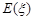 .
.