Question

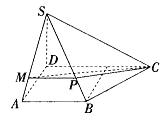
如图，四棱锥S—ABCD中，底面ABCD是直角梯形，∠BAD＝∠ADC＝90°，AB＝AD＝a，DC＝2a，SD＝a，SD⊥平面ABCD．

　　（1）证明：该四棱锥的四个侧面都是直角三角形；

　　（2）设M∈SA，SM＝x，平面CDMSB＝P，证明四边形CDMP也是直角梯形，并用a与x表示；

　　（3）x为何值时，CM最短，并求出其最短距离．

 

Answer 1

答案：
解析：

分析（1）△SDA、△SAB、△SDC显然是直角三角形，关键要证△SBC也是直角三角形，我们可以用勾股定理逆定理来证明；（2）证明CDMP是直角梯形关键要证MP∥CD，这就要证明CD∥平面SAB；（3）在Rt△CDM中利用勾股定理表示出，用二次函数极值求CM最短距离， 证明（1）SD⊥平面ABCDSD⊥DC，SD⊥DA， 　　 　　因此，△SDC、△SDA、△SAB是直角三角形． 　　∵  SA＝， 　　  BC＝， 　　  SB＝， 　　  SC＝， 　　∴  ， 　　∴  △SBC也是直角三角形，从而棱锥的四个侧面都是直角三角形．  　　CDMP是直角梯形． 　　∵  MP∥AB，∴  ， 　　MP＝， 　　， 　　 　　　　  ． 解  （3）∵  Rt△CDM中，∠CDM＝90°， 　　∴  　　　　　　 ， 　　因此，当x＝时，CM最小值为．

提示：