题目内容
已知:函数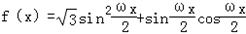 (ω>0)的周期为π.
(ω>0)的周期为π.
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)的单调递增区间.
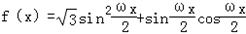 (ω>0)的周期为π.
(ω>0)的周期为π.(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)的单调递增区间.
解:(Ⅰ)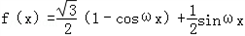 =
=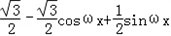
=﹣sin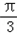 cosωx+
cosωx+ sinωx+
sinωx+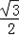 =
=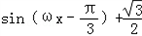
∴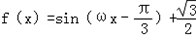
因为函数的周期为π
所以ω=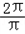 =2
=2
(Ⅱ)由(Ⅰ)知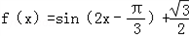
由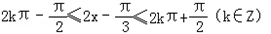 得:
得: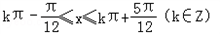
所以函数f(x)的单增区间为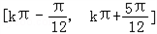 ,其中k∈Z
,其中k∈Z
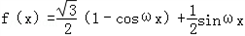 =
=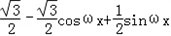
=﹣sin
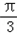 cosωx+
cosωx+ sinωx+
sinωx+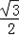 =
=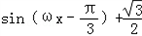
∴
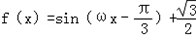
因为函数的周期为π
所以ω=
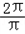 =2
=2(Ⅱ)由(Ⅰ)知
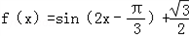
由
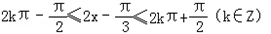 得:
得: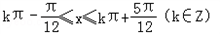
所以函数f(x)的单增区间为
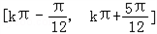 ,其中k∈Z
,其中k∈Z
练习册系列答案
相关题目
已知:函数f(x)=
,若a,b,c均不相等,且f(a)=f(b)=f(c),则a•b•c的取值范围是( )
|
| A、(0,9) |
| B、(2,9) |
| C、(9,11) |
| D、(2,11) |
(本题满分12分)探究函数 的最小值,并确定取得最小值时x的值. 列表如下, 请观察表中y值随x值变化的特点,完成以下的问题.
的最小值,并确定取得最小值时x的值. 列表如下, 请观察表中y值随x值变化的特点,完成以下的问题.
|
x |
… |
0.25 |
0.5 |
0.75 |
1 |
1.1 |
1.2 |
1.5 |
2 |
3 |
5 |
… |
|
y |
… |
8.063 |
4.25 |
3.229 |
3 |
3.028 |
3.081 |
3.583 |
5 |
9.667 |
25.4 |
… |
已知:函数 在区间(0,1)上递减,问:
在区间(0,1)上递减,问:
(1)函数 在区间
上递增.当
在区间
上递增.当 时,
时, ;
;
(2)函数 在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
 (a>0).解不等式:
(a>0).解不等式: .
. (a>0).解不等式:
(a>0).解不等式: .
. (a>0).解不等式:
(a>0).解不等式: .
.