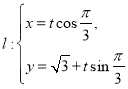题目内容
【题目】已知在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为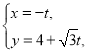 (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线l和曲线![]() 的极坐标方程;
的极坐标方程;
(2)曲线![]() 分别交直线和曲线
分别交直线和曲线![]() 于点
于点![]() ,求
,求![]() 的最大值及相应的
的最大值及相应的![]() 的值.
的值.
【答案】(1)![]() .
.![]() .(2)
.(2)![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
【解析】
(1)利用消参法将直线![]() 参数方程化为普通方程,利用互化公式
参数方程化为普通方程,利用互化公式![]() 和
和![]() ,将直线
,将直线![]() 和曲线
和曲线![]() 的直角坐标方程化为极坐标方程;
的直角坐标方程化为极坐标方程;
(2)由(1)得直线的极坐标方程为![]() ,令
,令![]() ,得出
,得出![]() ,
,![]() ,进而得出
,进而得出![]() ,利用降幂公式和辅助角公式,化简得
,利用降幂公式和辅助角公式,化简得![]() ,即可求得
,即可求得![]() 的最大值及相应的
的最大值及相应的![]() 的值.
的值.
解:(1)由题可知,直线l的参数方程为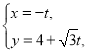 (
(![]() 为参数),
为参数),
消去参数,得出直线的普通方程为:![]() ,
,
利用互化公式![]() ,
,
则直线的极坐标方程为:![]() ,
,
由于曲线![]() 的普通方程为:
的普通方程为:![]() ,即:
,即:![]() ,
,
![]() 的极坐标方程为
的极坐标方程为![]() .
.
(2)直线的极坐标方程为![]() ,令
,令![]() ,
,
则![]() ,即
,即![]() ,
,
又![]() ,
,
![]()

![]() ,
,
即:![]()
![]() ,
,
![]() ,即当
,即当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】某班主任对全班50名学生学习积极性和对待工作的态度进行了调查,统计数据如下所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法有多大把握认为学生的学习积极性与对班级工作的态度有关系?并说明理由.
本题参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
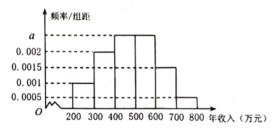
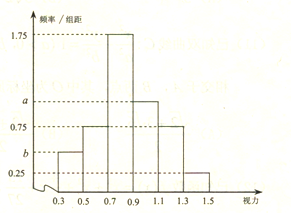
【题目】为了响应党的十九大所提出的教育教学改革,某校启动了数学教学方法的探索,学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班,每班40人,甲班按原有传统模式教学,乙班实施自主学习模式.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在![]() ,按照区间
,按照区间![]() ,
,![]() ,
,![]() ,
,![]() ,
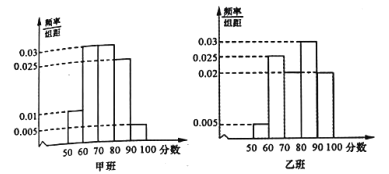
,![]() 进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
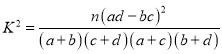
(1)完成表格,并判断是否有![]() 以上的把握认为“数学成绩优秀与教学改革有关”;
以上的把握认为“数学成绩优秀与教学改革有关”;
甲班 | 乙班 | 合计 | |
大于等于80分的人数 | |||
小于80分的人数 | |||
合计 |
(2)从乙班![]() ,
,![]() ,
,![]() 分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自
分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自![]() 发言的人数为随机变量
发言的人数为随机变量![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.