题目内容
已知椭圆 的对称中心为原点O,焦点在
的对称中心为原点O,焦点在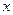 轴上,离心率为
轴上,离心率为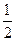 ,且点(1,
,且点(1,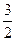 )在该椭圆上.
)在该椭圆上.
(I)求椭圆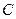 的方程;
的方程;
(II)过椭圆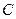 的左焦点
的左焦点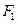 的直线
的直线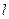 与椭圆
与椭圆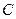 相交于
相交于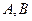 两点,若
两点,若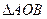 的面积为
的面积为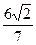 ,求圆心在原点O且与直线
,求圆心在原点O且与直线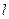 相切的圆的方
相切的圆的方 程.
程.
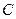 的对称中心为原点O,焦点在
的对称中心为原点O,焦点在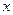 轴上,离心率为
轴上,离心率为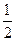 ,且点(1,
,且点(1,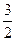 )在该椭圆上.
)在该椭圆上.(I)求椭圆
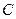 的方程;
的方程;(II)过椭圆
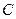 的左焦点
的左焦点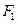 的直线
的直线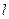 与椭圆
与椭圆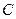 相交于
相交于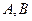 两点,若
两点,若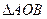 的面积为
的面积为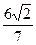 ,求圆心在原点O且与直线
,求圆心在原点O且与直线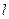 相切的圆的方
相切的圆的方 程.
程. (1)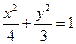 (2)
(2)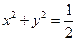
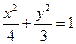 (2)
(2)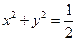
(I)设椭圆C的方程为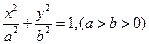 ,由题意可得
,由题意可得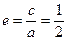 ,
,
又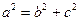 ,所以
,所以 ……………2分
……………2分
因为椭圆C经过(1,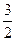 ),代入椭圆方程有
),代入椭圆方程有 
解得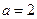 所以
所以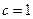 ,
,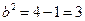 故椭圆C的方程为
故椭圆C的方程为 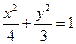 .………4分
.………4分
(Ⅱ)解法二:设直线 的方程为
的方程为 ,
,
由 ,消去x,得
,消去x,得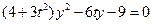
因为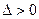 恒成立,设
恒成立,设 ,
,
则
 ……………6分
……………6分
所以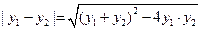
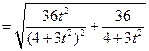
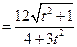 ……………8分
……………8分
所以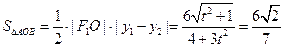
化简得到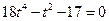 ,即
,即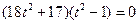 ,
,
解得

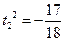 (舍)又圆
(舍)又圆 的半径为
的半径为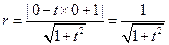 …10分
…10分
所以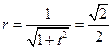 ,故圆
,故圆 的方程为:
的方程为: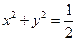 ……………12分
……………12分
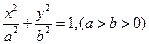 ,由题意可得
,由题意可得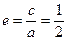 ,
, 又
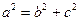 ,所以
,所以 ……………2分
……………2分因为椭圆C经过(1,
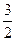 ),代入椭圆方程有
),代入椭圆方程有 
解得
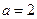 所以
所以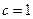 ,
,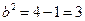 故椭圆C的方程为
故椭圆C的方程为 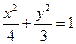 .………4分
.………4分 (Ⅱ)解法二:设直线
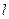 的方程为
的方程为 ,
,由
 ,消去x,得
,消去x,得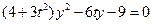
因为
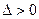 恒成立,设
恒成立,设 ,
,则

 ……………6分
……………6分所以
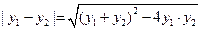
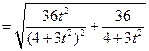
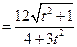 ……………8分
……………8分所以
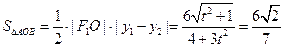
化简得到
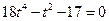 ,即
,即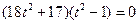 ,
,解得


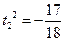 (舍)又圆
(舍)又圆 的半径为
的半径为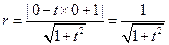 …10分
…10分所以
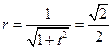 ,故圆
,故圆 的方程为:
的方程为: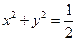 ……………12分
……………12分
练习册系列答案
相关题目
 的最大值.并求出此时b的值
的最大值.并求出此时b的值 在
在 轴上,抛物线上一点
轴上,抛物线上一点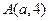 到准线的距离是
到准线的距离是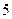 ,过点
,过点 ,
, 两点,过
两点,过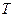 .
.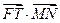 的值;
的值;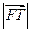 是
是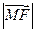 和
和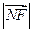 的等比中项.
的等比中项.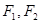 分别是双曲线的两个焦点,P为该曲线上一点,若
分别是双曲线的两个焦点,P为该曲线上一点,若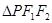 为等腰直角三角形,则该双曲线的离心率为( )
为等腰直角三角形,则该双曲线的离心率为( )



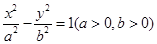 的两个顶点三等分焦距,则该双曲线的渐近线方程是
的两个顶点三等分焦距,则该双曲线的渐近线方程是



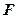 的直线l与抛物线C相交于A,B两点。若AB的中点为
的直线l与抛物线C相交于A,B两点。若AB的中点为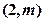 ,则弦
,则弦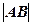 的长为_________。
的长为_________。
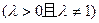 ,则动点M的轨迹是圆;
,则动点M的轨迹是圆;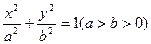 的离心率为
的离心率为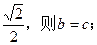
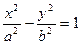
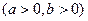 的焦点到渐近线的距离是
的焦点到渐近线的距离是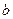 ;
;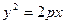 上两点
上两点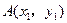 ,
, 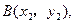 且
且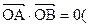
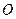 为原点),则
为原点),则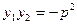 .
.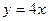 的焦点作直线
的焦点作直线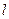 交抛物线于A、B两点,若线段AB中的横坐标为3,则|AB|等于 ( )
交抛物线于A、B两点,若线段AB中的横坐标为3,则|AB|等于 ( )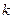 ,那么甲的面积是乙的面积的
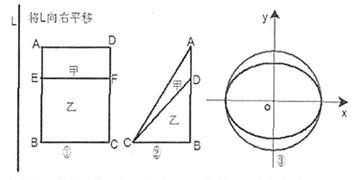
,那么甲的面积是乙的面积的 、乙:小矩形
、乙:小矩形 )、②(甲
)、②(甲 :大直角三角形
:大直角三角形 乙:小直角三角形
乙:小直角三角形 )中体会这个原理,现在图③中的曲线分别是
)中体会这个原理,现在图③中的曲线分别是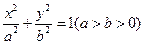 与
与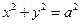 ,运用上面的原理,图③中椭圆的面积为 .
,运用上面的原理,图③中椭圆的面积为 .