题目内容
已知:以点C (t,  )(t∈R , t ≠ 0)为圆心的圆与
)(t∈R , t ≠ 0)为圆心的圆与 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N,若|OM| = |ON|,求圆C的方程.
【答案】
(1) 圆
圆 过原点
过原点 ,
, ,设圆
,设圆 的方程是
的方程是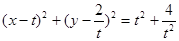
令 ,得
,得 ;令
;令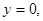 得
得
 ,即:
,即: 的面积为定值。
的面积为定值。
(2)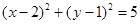
【解析】
试题分析:(1) 圆
圆 过原点
过原点 ,
,
设圆 的方程是
的方程是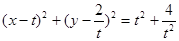
令 ,得
,得 ;令
;令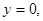 得
得
 ,即:
,即: 的面积为定值。
的面积为定值。
(2)
 ,
,  垂直平分线段
垂直平分线段

 ,
, ,
, 直线
直线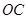 的方程是
的方程是
 ,解得:
,解得: 或
或
当 时,圆心
时,圆心 的坐标为
的坐标为 ,
, ,
,
此时 到直线
到直线
 的距离
的距离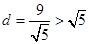 ,
,
圆 与直线
与直线 相交于两点.
相交于两点.
当 时,圆心
时,圆心 的坐标为
的坐标为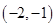 ,
, ,
,
此时 到直线
到直线 的距离
的距离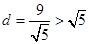
圆 与直线
与直线
 不相交,
不相交,
 不符合题意舍去.
不符合题意舍去.
圆 的方程为
的方程为
考点:圆的方程及直线与圆相交问题
点评:第一问要证三角形面积是定值首先要求出圆与坐标轴的交点,从而确定三角形边长;第二问由直线与圆相交的性质求得参数t后要验证此时圆与坐标轴是否相交,这一点容易忽略

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 )(t∈R , t ≠ 0)为圆心的圆与
)(t∈R , t ≠ 0)为圆心的圆与 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点. 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.