Question

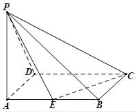在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠BAD=60°，侧棱PA⊥底面ABCD，PA=2，E为AB的中点，则四面体P-BCE的体积为

 

．

Answer 1

分析：根据四棱锥的特点求出三角形BCE的面积，即可根据锥体的体积公式计算体积．

解答：解：∵侧棱PA⊥底面ABCD，
∴PA是四面体P-BCE的高，
∵底面ABCD是边长为2的菱形，∠BAD=60°，
∴AB=BC=2，∠EBC=120°，
∵E为AB的中点，
∴BE=1，
∴三角形BCE的面积S=

1

2

×BE•BC•sin120°=

1

2

×1×2×

3

2

=

3

2

，
∴四面体P-BCE的体积为

1

3

•S△BCE•PA=

1

3

×

3

2

×2=

3

3

，
故答案为：

3

3

．

点评：本题主要考查三棱锥的体积的计算，利用条件求出三棱锥的底面积和高是解决本题的关键，要求熟练掌握锥体的体积公式．