题目内容
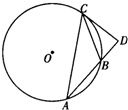
14、（选做题） 如图，圆 O 的割线 PBA 过圆心 O，弦 CD 交 PA 于点F，且△COF∽△PDF，PB=OA=2，则PF=3
．分析：由已知中OA=2，我们可得圆的半径为2，由相交弦定理及三角形相似的性质，我们可以得到AF•BF=OF•PF，结合PB=OA=2，求出BF长，进而即可求出PF的长．
解答：解：∵PB=OA=2，
∴OC=OB=2
由相交弦定理得：DF•CF=AF•BF
又∵△COF∽△PDF，
∴DF•CF=OF•PF
即AF•BF=OF•PF
即（4-BF）•BF=（2-BF）•（2+BF）
解得BF=1
故PF=PB+BF=3
故答案为：3
∴OC=OB=2
由相交弦定理得：DF•CF=AF•BF
又∵△COF∽△PDF，
∴DF•CF=OF•PF
即AF•BF=OF•PF
即（4-BF）•BF=（2-BF）•（2+BF）
解得BF=1
故PF=PB+BF=3
故答案为：3
点评：本题考查的知识点是相交弦定理及相似三角形的性质，其中根据相交弦定理及三角形相似的性质，得到AF•BF=OF•PF，是解答本题的关键．
练习册系列答案
相关题目
A．（不等式选做题）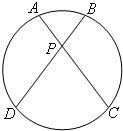
（几何证明选讲选选做题）如图，圆的两条弦AC、BD相交于P，弧AB、BC、CD、DA的度数分别为60°、105°、90°、105°，则
（几何证明选讲选做题）如图，圆O是△ABC的外接圆，过点C的切线交AB的延长线于点D，CD=2
选做题（请考生在以下三个小题中任选一题作答，如果多做，则按所做的第一题评阅记分）