题目内容
 已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的任意一点.
已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的任意一点.(1)求证:平面EBD⊥平面SAC;
(2)设SA=4,AB=2,求点A到平面SBD的距离.
分析:(1)证明平面EBD内的直线BD,垂直平面SAC内的两条相交直线AC,SA,即可证明平面EBD⊥平面SAC;
(2)SA=4,AB=2,设AC∩BD=F,连SF,点A到平面SBD的距离为h,利用
•S△SBD•h=
•S△ABD•SA,求点A到平面SBD的距离;
(2)SA=4,AB=2,设AC∩BD=F,连SF,点A到平面SBD的距离为h,利用
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:(1)∵SA⊥平面ABCD,BD?平面ABCD,
∴SA⊥BD、
∵ABCD是正方形,
∴AC⊥BD,∴BD⊥平面SAC、
∵BD?平面EBD,
∴平面EBD⊥平面SAC、
(2)设AC∩BD=F,连SF,则SF⊥BD、
∵AB=2.∴BD=2
.
∵SF=
=
=3
∴S△SBD=
BD•SF=
•2
•3
=6.
设点A到平面SBD的距离为h,
∵SA⊥平面ABCD,
∴
•S△SBD•h=
•S△ABD•SA,
∴6•h=
•2•2•4,
∴h=
,
∴点A到平面SBD的距离为
.
∴SA⊥BD、
∵ABCD是正方形,
∴AC⊥BD,∴BD⊥平面SAC、
∵BD?平面EBD,
∴平面EBD⊥平面SAC、
(2)设AC∩BD=F,连SF,则SF⊥BD、
∵AB=2.∴BD=2
| 2 |
∵SF=
| SA2+AF2 |
42+(
|
| 2 |
∴S△SBD=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
设点A到平面SBD的距离为h,
∵SA⊥平面ABCD,
∴
| 1 |
| 3 |
| 1 |
| 3 |
∴6•h=
| 1 |
| 2 |
∴h=
| 4 |
| 3 |
∴点A到平面SBD的距离为
| 4 |
| 3 |
点评:本题考查平面与平面垂直的判定,点、线、面间的距离计算,考查逻辑思维能力,转化思想,是中档题.

练习册系列答案
相关题目
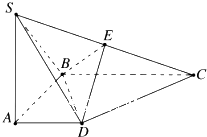 已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=