题目内容
已知关于x、y的二元一次线性方程组的增广矩阵是
,则该线性方程组有无穷多组解的充要条件是λ=( )
|
| A、2 | B、1或2 | C、1 | D、0 |
分析:将原方程组写成矩阵形式为Ax=b,其中A为2×2方阵,x为2个变量构成列向量,b为2个常数项构成列向量. 而当它的系数矩阵D奇异时,或者说行列式D=0时,方程组有无数个解或无解.由此求得λ值.
解答:解:系数矩阵D奇异时,或者说行列式D=0时,方程组有无数个解或无解.
∴系数行列式D=0,
即
=0.
解之得:a=1
故选C.
∴系数行列式D=0,
即
|
解之得:a=1
故选C.
点评:此题主要考查二元线性方程组的增广矩阵的涵义,计算量小,属于较容易的题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
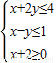 ,求函数z=x+2y+2的最大值和最小值.
,求函数z=x+2y+2的最大值和最小值.