题目内容
在边长为4的正三角形内任投一点，则该点到三边距离都不小于
的概率为
．
| ||
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
分析：在正三角形的内侧作三条平行线分别与三边平行，且距离等于
，可得到个小正三角形，可知落在小正三角形区域的点满足条件，所求概率即为小正三角形面积与大正三角形面积之比．
| ||
| 3 |
解答：解：在正三角形的内侧作三条平行线分别与三边平行，且距离等于
，可得到个小正三角形，可知落在小正三角形区域的点满足条件，所求概率即为小正三角形面积与大正三角形面积之比
∵大正三角形的边长为4
∴小正三角形高为
，大正三角形高2
∴两个三角形的面积比为1：4
故答案为：
| ||
| 3 |
∵大正三角形的边长为4
∴小正三角形高为
| 3 |
| 3 |
∴两个三角形的面积比为1：4
故答案为：
| 1 |
| 4 |
点评：本题考查几何概型，考查学生的计算能力，属于基础题．
练习册系列答案
习题精选系列答案
相关题目
如图所示，在边长为4的正三角形ABC中，E，F依次是AB，AC的中点，AD⊥BC，EH⊥BC，FG⊥BC，D，H，G为垂足，若将△ABC绕AD旋转180°，求阴影部分形成的几何体的表面积．
B. 
C.
D.
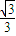的概率为 ．