题目内容
定义在R上的函数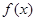 满足
满足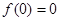 ,
,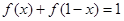 ,
,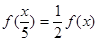 ,且当
,且当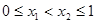 ,时,
,时,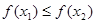 .
.
(1)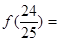 ;(2)
;(2)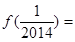 .
.
【答案】
(1)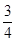 (2)
(2)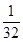
【解析】
试题分析:当x=0时,f(0)+f(1-0)=1,得f(1)=1;
当x=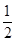 时,
时,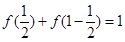 得f(
得f(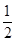 )=
)=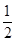 ;
;
由f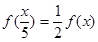 得f(
得f(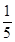 )=
)=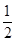 f(1)=
f(1)=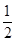 ;f(
;f(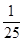 )=
)=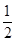 f(
f(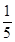 )=
)=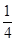 ;f(
;f(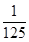 )=
)=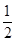 f(
f(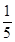 )=
)=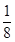 ;f(
;f(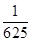 )=
)=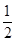 f(
f(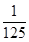 )=
)=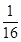 ;f(
;f(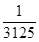 )=
)=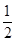 f(
f(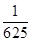 )=
)=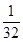 .
.
由f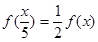 得f(
得f(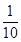 )=
)=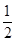 f(
f(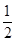 )=
)=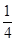 ;f(
;f(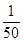 )=
)=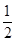 f(
f(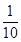 )=
)=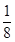 ;f(
;f(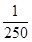 )=
)=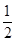 f(
f(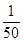 )=
)=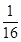 ;
;
f(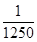 )=
)=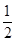 f(
f(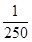 )=
)=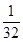 ;
;
又因为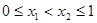 ,时,
,时,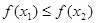 .
.
所以f(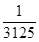 )
)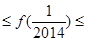 f(
f(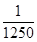 )
)
而f(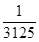 )=f(
)=f(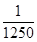 )=
)=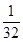 且函数在(0,1)上是单调增函数,所以
且函数在(0,1)上是单调增函数,所以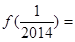
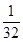 ,
,
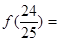 1- f(
1- f(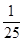 )=1-
)=1-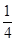 =
=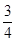 .
.
考点:1.抽象函数;2.函数的单调性.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目