题目内容
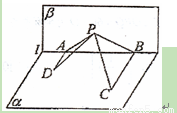
如图,平面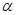 ⊥平面
⊥平面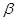 ,
,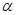 ∩
∩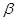 =
=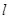 ,DA
,DA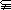
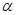 ,BC
,BC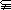
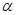 ,且DA⊥
,且DA⊥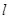 于A,BC⊥
于A,BC⊥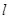 于B,AD=4,BC=8,AB=6,在平面
于B,AD=4,BC=8,AB=6,在平面 内不在
内不在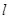 上的动点P,记PD与平面
上的动点P,记PD与平面 所成角为
所成角为 ,PC与平面
,PC与平面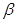 所成角为
所成角为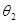 ,若
,若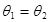 ,则△PAB的面积的最大值是
。
,则△PAB的面积的最大值是
。
【答案】
12
【解析】由条件可得:PB=2PA,即P到B的距离为到A的距离的2倍
在平面 内以AB为
内以AB为 轴,AB的中垂线为
轴,AB的中垂线为 轴,建立平面直角坐标系
轴,建立平面直角坐标系
设P( ,
, )则
)则 =
=
∴ =
= ∴
∴ +27=0
+27=0
∴ ∴
∴ =16
=16
∴平面 内P点轨迹为以(
内P点轨迹为以( ,0)为圆心,4为半径的圆(与
,0)为圆心,4为半径的圆(与 轴的交点除外)
轴的交点除外)
∴高的最大值为4,
∴面积的最大值为 =12
=12

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,已知等腰△ABC的底边BC=3,顶角为120°,D是BC边上一点,且BD=1.把△ADC沿AD折起,使得平面CAD⊥平面ABD,连接BC形成三棱锥C-ABD.
如图,已知等腰△ABC的底边BC=3,顶角为120°,D是BC边上一点,且BD=1.把△ADC沿AD折起,使得平面CAD⊥平面ABD,连接BC形成三棱锥C-ABD.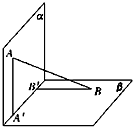 如图,平面α⊥平面β,A∈α,B∈β,AB与平面α、β所成的角分别为
如图,平面α⊥平面β,A∈α,B∈β,AB与平面α、β所成的角分别为
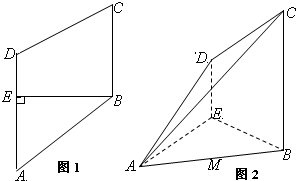 (2013•威海二模)如图1,在梯形ABCD中,BC∥DA,BE⊥DA,EA=EB=BC=2,DE=1,将四边形DEBC沿BE折起,使平面DEBC垂直平面ABE,如图2,连结AD,AC.设M是AB上的动点.
(2013•威海二模)如图1,在梯形ABCD中,BC∥DA,BE⊥DA,EA=EB=BC=2,DE=1,将四边形DEBC沿BE折起,使平面DEBC垂直平面ABE,如图2,连结AD,AC.设M是AB上的动点. 如图,平面
如图,平面