题目内容

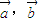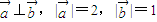设平面内两向量满足：，点M（x，y）的坐标满足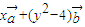：与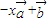互相垂直．求证：平面内存在两个定点A、B，使对满足条件的任意一点M均有|等于定值．
【答案】分析：由已知可得，把已知条件代入整理可得M的轨迹是双曲线，由双曲线的定义可知，满足条件的点即为双曲线的两焦点，而定值即为双曲线的实轴长2a
解答：证明：∵，∴
∵与垂直，且
∴
∴
整理可得
M（x，y）的轨迹是以（0，）（0，-）为焦点的双曲线
由双曲线的定义可知当A，B分别为该双曲线的焦点时，||MA|-|MB||=4
点评：本题以向量垂直为切入点，综合考查双曲线的定义的应用，灵活熟练的推理论证及对基本知识的掌握是解决本题的关键．
练习册系列答案
相关题目
设平面内两向量
a
，
b
满足：
a
⊥
b
，|
a
|=2，|
b
|=1，点M（x，y）的坐标满足：x
a
+(y2-4)
b
与-x
a
+
b
互相垂直．求证：平面内存在两个定点A、B，使对满足条件的任意一点M均有|||
MA
|-|
MB
||等于定值．
给出以下5个命题：
①曲线x2-（y-1）2=1按
a
=(1，-2)平移可得曲线（x+1）2-（y-3）2=1；
②设A、B为两个定点，n为常数，|
PA
|-|
PB
|=n，则动点P的轨迹为双曲线；
③若椭圆的左、右焦点分别为F1、F2，P是该椭圆上的任意一点，延长F1P到点M，使|F2P|=|PM|，则点M的轨迹是圆；
④A、B是平面内两定点，平面内一动点P满足向量
AB
与
AP
夹角为锐角θ，且满足 |
PB
| |
AB
| +
PA
•
AB
=0，则点P的轨迹是圆（除去与直线AB的交点）；
⑤已知正四面体A-BCD，动点P在△ABC内，且点P到平面BCD的距离与点P到点A的距离相等，则动点P的轨迹为椭圆的一部分．
其中所有真命题的序号为
 
．
（2012•闸北区一模）设
a
、
b
为平面内两个互相垂直的单位向量，向量
c
满足(
c
+
a
)•(
c
-
b
)=0，则|
c
|的最大值为
2
2
．

设平面内两向量a、b满足：a⊥b，｜a｜＝2，｜b｜＝1，点M(x，y)的坐标满足：xa＋(y2－4)b与－xa＋b互相垂直．

求证：平面内存在两个定点A、B，使对满足条件的任意一点M均有｜｜｜－｜｜｜等于定值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网